 Embryo series courtesy of Einhard Schierenberg
Embryo series courtesy of Einhard SchierenbergTable of Contents
Abstract
The proper understanding and use of statistical tools are essential to the scientific enterprise. This is true both at the level of designing one's own experiments as well as for critically evaluating studies carried out by others. Unfortunately, many researchers who are otherwise rigorous and thoughtful in their scientific approach lack sufficient knowledge of this field. This methods chapter is written with such individuals in mind. Although the majority of examples are drawn from the field of Caenorhabditis elegans biology, the concepts and practical applications are also relevant to those who work in the disciplines of molecular genetics and cell and developmental biology. Our intent has been to limit theoretical considerations to a necessary minimum and to use common examples as illustrations for statistical analysis. Our chapter includes a description of basic terms and central concepts and also contains in-depth discussions on the analysis of means, proportions, ratios, probabilities, and correlations. We also address issues related to sample size, normality, outliers, and non-parametric approaches.
At the first group meeting that I attended as a new worm postdoc (1997, D.S.F.), I heard the following opinion expressed by a senior scientist in the field: “If I need to rely on statistics to prove my point, then I'm not doing the right experiment.” In fact, reading this statement today, many of us might well identify with this point of view. Our field has historically gravitated toward experiments that provide clear-cut “yes” or “no” types of answers. Yes, mutant X has a phenotype. No, mutant Y does not genetically complement mutant Z. We are perhaps even a bit suspicious of other kinds of data, which we perceive as requiring excessive hand waving. However, the realities of biological complexity, the sometimes-necessary intrusion of sophisticated experimental design, and the need for quantifying results may preclude black-and-white conclusions. Oversimplified statements can also be misleading or at least overlook important and interesting subtleties. Finally, more and more of our experimental approaches rely on large multi-faceted datasets. These types of situations may not lend themselves to straightforward interpretations or facile models. Statistics may be required.
The intent of these sections will be to provide C. elegans researchers with a practical guide to the application of statistics using examples that are relevant to our field. Namely, which common situations require statistical approaches and what are some of the appropriate methods (i.e., tests or estimation procedures) to carry out? Our intent is therefore to aid worm researchers in applying statistics to their own work, including considerations that may inform experimental design. In addition, we hope to provide reviewers and critical readers of the worm scientific literature with some criteria by which to interpret and evaluate statistical analyses carried out by others. At various points we suggest some general guidelines, which may lead to somewhat more uniformity in how our field conducts and presents statistical findings. Finally, we provide some suggestions for additional readings for those interested in a more systematic and in-depth coverage of the topics introduced (Appendix A).
There are numerous ways to describe and present the variation that is inherent to most data sets. Range (defined as the largest value minus the smallest) is one common measure and has the advantage of being simple and intuitive. Range, however, can be misleading because of the presence of outliers, and it tends to be larger for larger sample sizes even without unusual data values. Standard deviation (SD) is the most common way to present variation in biological data. It has the advantage that nearly everyone is familiar with the term and that its units are identical to the units of the sample measurement. Its disadvantage is that few people can recall what it actually means.
Figure 1 depicts density curves of brood sizes in two different populations of self-fertilizing hermaphrodites. Both have identical average brood sizes of 300. However, the population in Figure 1B displays considerably more inherent variation than the population in Figure 1A. Looking at the density curves, we would predict that 10 randomly selected values from the population depicted in Figure 1B would tend to show a wider range than an equivalent set from the more tightly distributed population in Figure 1A. We might also note from the shape and symmetry of the density curves that both populations are Normally1 distributed (this is also referred to as a Gaussian distribution). In reality, most biological data do not conform to a perfect bell-shaped curve, and, in some cases, they may profoundly deviate from this ideal. Nevertheless, in many instances, the distribution of various types of data can be roughly approximated by a normal distribution. Furthermore, the normal distribution is a particularly useful concept in classical statistics (more on this later) and in this example is helpful for illustrative purposes.
The vertical red lines in Figure 1A and 1B indicate one SD to either side of the mean. From this, we can see that the population in Figure 1A has a SD of 20, whereas the population in Figure 1B has a SD of 50. A useful rule of thumb is that roughly 67% of the values within a normally distributed population will reside within one SD to either side of the mean. Correspondingly, 95% of values reside within two2 SDs, and more than 99% reside within three SDs to either side of the mean. Thus, for the population in Figure 1A, we can predict that about 95% of hermaphrodites produce brood sizes between 260 and 340, whereas for the population in Figure 1B, 95% of hermaphrodites produce brood sizes between 200 and 400.
Often we can never really know the true mean or SD of a population because we cannot usually observe the entire population. Instead, we must use a sample to make an educated guess. In the case of experimental laboratory science, there is often no limit to the number of animals that we could theoretically test or the number of experimental repeats that we could perform. Admittedly, use of the term “populations” in this context can sound rather forced. It's awkward for us to think of a theoretical collection of bands on a western blot or a series of cycle numbers from a qRT-PCR experiment as a population, but from the standpoint of statistics, that's exactly what they are. Thus, our populations tend to be mythical in nature as well as infinite. Moreover, even the most sadistic advisor can only expect a finite number of biological or technical repeats to be carried out. The data that we ultimately analyze are therefore always just a tiny proportion of the population, real or theoretical, from whence they came.
It is important to note that increasing our sample size will not predictably increase or decrease the amount of variation that we are ultimately likely to record. What can be stated is that a larger sample size will tend to give a sample SD that is a more accurate estimate of the population SD. In the same vein, a larger sample size will also provide a more accurate estimation of other parameters, such as the population mean.
In some cases, standard numerical summaries (e.g., mean and SD) may not be sufficient to fully or accurately describe the data. In particular, these measures usually3 tell you nothing about the shape of the underlying distribution. Figure 2 illustrates this point; Panels A and B show the duration (in seconds) of vulval muscle cell contractions in two populations of C. elegans. The data from both panels have nearly identical means and SDs, but the data from panel A are clearly bimodal, whereas the data from Panel B conform more to a normal distribution4. One way to present this observation would be to show the actual histograms (in a figure or supplemental figure). Alternatively, a somewhat more concise depiction, which still gets the basic point across, is shown by the individual data plot in Panel C. In any case, presenting these data simply as a mean and SD without highlighting the difference in distributions would be potentially quite misleading, as the populations would appear to be identical.
Figure 2. Two distributions with similar means and SDs. Panels A and B show histograms of simulated data of vulval muscle cell contraction durations derived from underlying populations with distributions that are either bimodal (A) or normal (B). Note that both populations have nearly identical means and SDs, despite major differences in the population distributions. Panel C displays the same information shown in the two histograms using individual data plots. Horizontally arrayed sets of dots represent repeat values.
Before you become distressed about what the title of this section actually means, let's be clear about something. Statistics, in its broadest sense, effectively does two things for us—more or less simultaneously. (1) Statistics provides us with useful quantitative descriptors for summarizing our data. This includes fairly simple stuff such as means and proportions. It also includes more complex statistics such as the correlation between related measurements, the slope of a linear regression, and the odds ratio for mortality under differing conditions. These can all be useful for interpreting our data, making informed conclusions, and constructing hypotheses for future studies. However, statistics gives us something else, too. (2) Statistics also informs us about the accuracy of the very estimates that we've made. What a deal! Not only can we obtain predictions for the population mean and other parameters, we also estimate how accurate those predictions really are. How this comes about is part of the “magic” of statistics, which as stated shouldn't be taken literally, even if it appears to be that way at times.
In the preceding section we discussed the importance of SD as a measure for describing natural variation within an entire population of worms. We also touched upon the idea that we can calculate statistics, such as SD, from a sample that is drawn from a larger population. Intuition also tells us that these two values, one corresponding to the population, the other to the sample, ought to generally be similar in magnitude, if the sample size is large. Finally, we understand that the larger the sample size, the closer our sample statistic will be to the true population statistic. This is true not only for the SD but also for many other statistics as well.
It is now time to discuss SD in another context that is central to the understanding of statistics. We do this with a thought experiment. Imagine that we determine the brood size for six animals that are randomly selected from a larger population. We could then use these data to calculate a sample mean, as well as a sample SD, which would be based on a sample size of n = 6. Not being satisfied with our efforts, we repeat this approach every day for 10 days, each day obtaining a new mean and new SD (Table 1). At the end of 10 days, having obtained ten different means, we can now use each sample mean as though it were a single data point to calculate a new mean, which we can call the mean of the means. In addition, we can calculate the SD of these ten mean values, which we can refer to for now as the SD of the means. We can then pose the following question: will the SD calculated using the ten means generally turn out to be a larger or smaller value (on average) than the SD calculated from each sample of six random individuals? This is not merely an idiosyncratic question posed for intellectual curiosity. The notion of the SD of the mean is critical to statistical inference. Read on.
Table 1. Ten random samples (trials) of brood sizes.
| Trial | Brood Sizesa | Sample Mean | Sample SD | SEb of Mean | |||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||||
| 1 | 218 | 259 | 271 | 320 | 266 | 392 | 287.67 | 60.59 | 24.73 |
| 2 | 370 | 237 | 307 | 358 | 295 | 318 | 314.17 | 47.81 | 19.52 |
| 3 | 324 | 264 | 343 | 269 | 304 | 223 | 287.83 | 44.13 | 18.02 |
| 4 | 341 | 343 | 277 | 374 | 302 | 308 | 324.17 | 34.93 | 14.26 |
| 5 | 293 | 362 | 296 | 384 | 270 | 307 | 318.67 | 44.32 | 18.10 |
| 6 | 366 | 301 | 209 | 336 | 254 | 295 | 293.50 | 56.25 | 22.96 |
| 7 | 325 | 240 | 304 | 294 | 260 | 310 | 288.83 | 32.34 | 13.20 |
| 8 | 334 | 327 | 310 | 346 | 320 | 233 | 311.67 | 40.43 | 16.56 |
| 9 | 339 | 256 | 240 | 329 | 230 | 361 | 292.50 | 56.89 | 23.22 |
| 10 | 235 | 300 | 271 | 300 | 281 | 253 | 273.33 | 25.96 | 10.60 |
| Mean of values | 299.2 | 44.36 | 18.11 | ||||||
| SD of means | 16.66 | ||||||||
|
aFor each trial, n = 6 worms were assayed for brood size. bSE, standard error. When applied to a mean value, also abbreviated as SEM. |
|||||||||
Thinking about this, we may realize that the ten mean values, being averages of six worms, will tend to show less total variation than measurements from individual worms. In other words, the variation between means should be less than the variation between individual data values. Moreover, the average of these means will generally be closer to the true population mean than would a mean obtained from just six random individuals. In fact, this idea is born out in Table 1, which used random sampling from a theoretical population (with a mean of 300 and SD of 50) to generate the sample values. We can therefore conclude sample means will generally exhibit less variation than that seen among individual samples. Furthermore, we can consider what might happen if we were to take daily samples of 20 worms instead of 6. Namely, the larger sample size would result in an even tighter cluster of mean values. This in turn would produce an even smaller SD of the means than from the experiment where only six worms were analyzed each day. Thus, increasing sample size will consistently lead to a smaller SD of the means. Note however, as discussed above, increasing sample size will not predictably lead to a smaller or larger SD for any given sample.
It turns out that this concept of calculating the SD of multiple means (or other statistical parameters) is a very important one. The good news is that rather than having to actually collect samples for ten or more days, statistical theory gives us a short cut that allows us to estimate this value based on only a single day's effort. What a deal! Rather than calling this value the “SD of the means”, as might make sense, the field has historically chosen to call this value the “standard error of the mean” (SEM). In fact, whenever a SD is calculated for a statistic (e.g., the slope from a regression or a proportion), it is called the standard error (SE) of that statistic. SD is a term generally reserved for describing variation within a sample or population only. Although we will largely avoid the use of formulas in this review, it is worth knowing that we can estimate the SEM from a single sample of n animals using the following equation:
From this relatively simple formula5, we can see that the greater the SD of the sample, the greater the SEM will be. Conversely, the larger our sample size, the smaller the SEM will be. Looking back at Table 1, we can also see that the SEM estimate for each daily sample is reasonably6 close, on average, to what we obtained by calculating the observed SD of the means from 10 days. This is not an accident. Rather, chalk one up for statistical theory.
Obviously, having a smaller SEM value reflects more precise estimates of the population mean. For that reason, scientists are typically motivated to keep SEM values as low as possible. In the case of experimental biology, variation within our samples may be due to inherent biological variation or to technical issues related to the methods we use. The former we probably can't control very much. The latter we may be able to control to some extent, but probably not completely. This leaves increasing sample size as a direct route to decreasing SE estimates and thus to improving the precision of the parameter estimates. However, increasing sample size in some instances may not be a practical or efficient use of our time. Furthermore, because the denominator in SE equations typically involves the square root of sample size, increasing sample size will have diminishing returns. In general, a quadrupling of sample size is required to yield a halving of the SEM. Moreover, as discussed elsewhere in this chapter, supporting very small differences with very high sample sizes might lead us to make convincing-sounding statistical statements regarding biological effects of no real importance, which is not something we should aspire to do.
Although SDs and SEs are all well and good, what we typically want to know is the accuracy of our parameter estimates. It turns out that SEs are the key to calculating a more directly useful measure, a confidence interval (CI). Although, the transformation of SEs into CIs isn't necessarily that complex, we will generally want to let computers or calculators perform this conversion for us. That said, for sample means derived from sample sizes greater than about ten, a 95% CI will usually span about two SEMs above and below the mean7. When pressed for a definition, most people might say that with a 95% CI, we are 95% certain that the true value of the mean or slope (or whatever parameter we are estimating) is between the upper and lower limits of the given CI. Proper statistical semantics would more accurately state that a 95% CI procedure is such that 95% of properly calculated intervals from appropriately random samples will contain the true value of the parameter. If you can discern the difference, fine. If not, don't worry about it.
One thing to keep in mind about CIs is that, for a given sample, a higher confidence level (e.g., 99%) will invoke intervals that are wider than those created with a lower confidence level (e.g., 90%). Think about it this way. With a given amount of information (i.e., data), if you wish to be more confident that your interval contains the parameter, then you need to make the interval wider. Thus, less confidence corresponds to a narrower interval, whereas higher confidence requires a wider interval. Generally for CIs to be useful, the range shouldn't be too great. Another thing to realize is that there is really only one way to narrow the range associated with a given confidence level, and that is to increase the sample size. As discussed above, however, diminishing returns, as well as basic questions related to biological importance of the data, should figure foremost in any decision regarding sample size.
Of course, the answer to this will depend on what you are trying to show and which measures of variation are most relevant to your experiment. Nevertheless, here is an important news flash: with respect to means, the SEM is often not the most informative parameter to display. This should be pretty obvious by now. SD is a good way to go if we are trying to show how much variation there is within a population or sample. CIs are highly informative if we are trying to make a statement regarding the accuracy of the estimated population mean. In contrast, SEM does neither of these things directly, yet remains very popular and is often used inappropriately (Nagele, 2003). Some statisticians have pointed out that because SEM gives the smallest of the error bars, authors may often chose SEMs for aesthetic reasons. Namely, to make their data appear less variable or to convince readers of a difference between values that might not otherwise appear to be very different. In fairness, SEM is a perfectly legitimate descriptor of variation8. In contrast to CIs, the size of the SEM is not an artifact of the chosen confidence level. Furthermore, unlike the CI, the validity of the SEM does not require assumptions that relate to statistical normality9. However, because the SEM is often less directly informative to readers, presenting either SDs or CIs can be strongly recommended for most data. Furthermore, if the intent of a figure is to compare means for differences or a lack thereof, CIs are the clear choice.
Figure 3 shows a bar graph containing identical (artificial) data plotted with the SD, SEM, and CI to indicate variation. Note that the SD is the largest value, followed by the CI and SEM. This will be the case for all but very small sample sizes (in which case the CI could be wider than two SDs). Remember: SD is variation among individuals, SE is the variation for a theoretical collection of sample means (acquired in an identical manner to the real sample), and CI is a rescaling of the SE so as to be able to impute confidence regarding the value of the population mean. With larger sample sizes, the SE and CI will shrink, but there is no such tendency for the SD, which tends to remain the same but can also increase or decrease somewhat in a manner that is not predictable.
Figure 4 shows two different situations for two artificial means: one in which bars do not overlap (Figure 4A), and one in which they do, albeit slightly (Figure 4B). The following are some general guidelines for interpreting error bars, which are summarized in Table 2. (1) With respect to SD, neither overlapping bars nor an absence of overlapping bars can be used to infer whether or not two sample means are significantly different. This again is because SD reflects individual variation and you simply cannot infer anything about significance of differences for the means. End of story. (2) With respect to SEM, overlapping bars (Figure 4B) can be used to infer that the sample means are not significantly different. However, the absence of overlapping bars (Figure 4A) cannot be used to infer that the sample means are different. (3) With respect to CIs, the absence of overlapping bars (Figure 4A) can be used to infer that the sample means are statistically different6. If the CI bars do overlap (Figure 4B), however, the answer is “maybe”. Here is why. The correct measure for comparing two means is in fact the SE of the difference between the means. In the case of equal SEMs, as illustrated in Figure 4, the SE of the difference is ∼1.4 times the SEM. To be significantly different,10 then, two means need to be separated by about twice the SE of the difference (2.8 SEMs). In contrast, visual separation using the CI bars requires a difference of four times the SEM (remember that CI ∼ 2 × SEM above and below the mean), which is larger than necessary to infer a difference between means. Therefore, a slight overlap can be present even when two means differ significantly. If they overlap a lot (e.g., the CI for Mean 1 includes Mean 2), then the two means are for sure not significantly different. If there is any uncertainty (i.e., there is some slight overlap), determination of significance is not possible; the test needs to be formally carried out.
Table 2. General guidelines for interpreting error bars.
| Error bar type | Overlapping error bars | Non-overlapping error bars |
|---|---|---|
| SD | no inference | no inference |
| SEM | sample means are not significantly different | no inference |
| CI | sample means may or may not be significantly different | sample means are significantly different |
In some cases, it may be most relevant to describe the relative variation within a sample or population. Put another way, knowing the sample SD is really not very informative unless we also know
the sample mean. Thus, a sample with a SD = 50 and mean = 100 shows considerably more relative variation than a sample with
SD = 100 but mean = 10,000. To indicate the level of variation relative to the mean, we can report the coefficient of variation
(CV). In the case of sample means (![]() ), this can be calculated as follows:
), this can be calculated as follows:
Thus, low CVs indicate relatively little variation within the sample, and higher CVs indicate more variation. In addition,
because units will cancel out in this equation, CV is a unitless expression. This is actually advantageous when comparing
relative variation between parameters that are described using different scales or distinct types of measurements. Note, however,
that in situations where the mean value is zero (or very close to zero), the CV could approach infinity and will not provide
useful information. A similar warning applies in cases when data can be negative. The CV is most useful and meaningful only
for positively valued data. A variation on the CV is its use as applied to a statistic (rather than to individual variation).
Then its name has to reflect the statistic in question; so, for example,
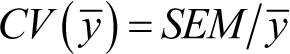 . For another example (the role of
. For another example (the role of
![]() may be confusing here), suppose one has estimated a proportion (mortality, for instance), and obtained an estimate labeled
may be confusing here), suppose one has estimated a proportion (mortality, for instance), and obtained an estimate labeled
![]() and its SE, labeled
and its SE, labeled
![]() . Then
. Then 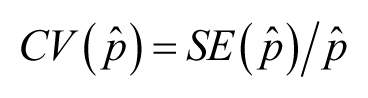
Most statistical tests culminate in a statement regarding the P-value, without which reviewers or readers may feel shortchanged. The P-value is commonly defined as the probability of obtaining a result (more formally a test statistic) that is at least as extreme as the one observed, assuming that the null hypothesis is true. Here, the specific null hypothesis will depend on the nature of the experiment. In general, the null hypothesis is the statistical equivalent of the “innocent until proven guilty” convention of the judicial system. For example, we may be testing a mutant that we suspect changes the ratio of male-to-hermaphrodite cross-progeny following mating. In this case, the null hypothesis is that the mutant does not differ from wild type, where the sex ratio is established to be 1:1. More directly, the null hypothesis is that the sex ratio in mutants is 1:1. Furthermore, the complement of the null hypothesis, known as the experimental or alternative hypothesis, would be that the sex ratio in mutants is different than that in wild type or is something other than 1:1. For this experiment, showing that the ratio in mutants is significantly different than 1:1 would constitute a finding of interest. Here, use of the term “significantly” is short-hand for a particular technical meaning, namely that the result is statistically significant, which in turn implies only that the observed difference appears to be real and is not due only to random chance in the sample(s). Whether or not a result that is statistically significant is also biologically significant is another question. Moreover, the term significant is not an ideal one, but because of long-standing convention, we are stuck with it. Statistically plausible or statistically supported may in fact be better terms.
Getting back to P-values, let's imagine that in an experiment with mutants, 40% of cross-progeny are observed to be males, whereas 60% are hermaphrodites. A statistical significance test then informs us that for this experiment, P = 0.25. We interpret this to mean that even if there was no actual difference between the mutant and wild type with respect to their sex ratios, we would still expect to see deviations as great, or greater than, a 6:4 ratio in 25% of our experiments. Put another way, if we were to replicate this experiment 100 times, random chance would lead to ratios at least as extreme as 6:4 in 25 of those experiments. Of course, you may well wonder how it is possible to extrapolate from one experiment to make conclusions about what (approximately) the next 99 experiments will look like. (Short answer: There is well-established statistical theory behind this extrapolation that is similar in nature to our discussion on the SEM.) In any case, a large P-value, such as 0.25, is a red flag and leaves us unconvinced of a difference. It is, however, possible that a true difference exists but that our experiment failed to detect it (because of a small sample size, for instance). In contrast, suppose we found a sex ratio of 6:4, but with a corresponding P-value of 0.001 (this experiment likely had a much larger sample size than did the first). In this case, the likelihood that pure chance has conspired to produce a deviation from the 1:1 ratio as great or greater than 6:4 is very small, 1 in 1,000 to be exact. Because this is very unlikely, we would conclude that the null hypothesis is not supported and that mutants really do differ in their sex ratio from wild type. Such a finding would therefore be described as statistically significant on the basis of the associated low P-value.
There is a long-standing convention in biology that P-values that are ≤0.05 are considered to be significant, whereas P-values that are >0.05 are not significant11. Of course, common sense would dictate that there is no rational reason for anointing any specific number as a universal cutoff, below or above which results must either be celebrated or condemned. Can anyone imagine a convincing argument by someone stating that they will believe a finding if the P-value is 0.04 but not if it is 0.06? Even a P-value of 0.10 suggests a finding for which there is some chance that it is real.
So why impose “cutoffs”, which are often referred to as the chosen α level, of any kind? Well, for one thing, it makes life simpler for reviewers and readers who may not want to agonize over personal judgments regarding every P-value in every experiment. It could also be argued that, much like speed limits, there needs to be an agreed-upon cutoff. Even if driving at 76 mph isn't much more dangerous than driving at 75 mph, one does have to consider public safety. In the case of science, the apparent danger is that too many false-positive findings may enter the literature and become dogma. Noting that the imposition of a reasonable, if arbitrary, cutoff is likely to do little to prevent the publication of dubious findings is probably irrelevant at this point.
The key is not to change the chosen cutoff—we have no better suggestion12 than 0.05. The key is for readers to understand that there is nothing special about 0.05 and, most importantly, to look beyond P-values to determine whether or not the experiments are well controlled and the results are of biological interest. It is also often more informative to include actual P-values rather than simply stating P ≤ 0.05; a result where P = 0.049 is roughly three times more likely to have occurred by chance than when P = 0.016, yet both are typically reported as P ≤ 0.05. Moreover, reporting the results of statistical tests as P ≤ 0.05 (or any number) is a holdover to the days when computing exact P-values was much more difficult. Finally, if a finding is of interest and the experiment is technically sound, reviewers need not skewer a result or insist on authors discarding the data just because P ≤ 0.07. Judgment and common sense should always take precedent over an arbitrary number.
1In theory, we could always capitalize “Normal” to emphasize its role as the name of a distribution, not a reference to “normal”, meaning usual or typical. However, most texts don't bother and so we won't either.
2A useful addendum: Four SDs captures the range of most (here, formally 95%) data values; it turns out this is casually true for the distribution for most real-life variables (i.e., not only those that are normally distributed). Most (but not quite all) of the values will span a range of approximately four SDs.
3For example, in many instances, data values are known to be composed of only non-negative values. In that instance, if the coefficient of variation (SD/mean) is greater than ∼0.6, this would indicate that the distribution is skewed right.
4Indeed the data from Panel B was generated from a normal distribution. However, you can see that the distribution of the sample won't necessarily be perfectly symmetric and bell-shape, though it is close. Also note that just because the distribution in Panel A is bimodal does not imply that classical statistical methods are inapplicable. In fact, a simulation study based on those data showed that the distribution of the sample mean was indeed very close to normal, so a usual t-based confidence interval or test would be valid. This is so because of the large sample size and is a predictable consequence of the Central Limit Theorem (see Section 2 for a more detailed discussion).
5We note that the SE formula shown here is for the SE of a mean from a random sample. Changing the sample design (e.g., using stratified sampling) or choosing a different statistic requires the use of a different formula.
6Our simulation had only ten random samples of size six. Had we used a much larger number of trials (e.g., 100 instead of 10), these two values would have been much closer to each other.
7This calculation (two times the SE) is sometimes called the margin of error for the CI.
8Indeed, given the ubiquity of “95%” as a usual choice for confidence level, and applying the concept in Footnote 2, a quick-and-dirty “pretty darn sure” (PDS) CI can be constructed by using 2 times the SE as the margin of error. This will approximately coincide with a 95% CI under many circumstances, as long as the sample size is not small.
9The requirement for normality in the context of various tests will be discussed in later sections.
10Here meaning by a statistical test where the P-value cutoff or “alpha level” (α) is 0.05.
11R.A. Fisher, a giant in the field of statistics, chose this value as being meaningful for the agricultural experiments with which he worked in the 1920s.
12Although one of us is in favor of 0.056, as it coincides with his age (modulo a factor of 1000).
Many studies in our field boil down to generating means and comparing them to each other. In doing so, we try to answer questions such as, “Is the average brood size of mutant x different from that of wild type?” or “Is the expression of gene y in embryos greater at 25 °C than at 20 °C?” Of course we will never really obtain identical values from any two experiments. This is true even if the data are acquired from a single population; the sample means will always be different from each other, even if only slightly. The pertinent question that statistics can address is whether or not the differences we inevitably observe reflect a real difference in the populations from which the samples were acquired. Put another way, are the differences detected by our experiments, which are necessarily based on a limited sample size, likely or not to result from chance effects of sampling (i.e., chance sampling). If chance sampling can account for the observed differences, then our results will not be deemed statistically significant13. In contrast, if the observed differences are unlikely to have occurred by chance, then our results may be considered significant in so much as statistics are concerned. Whether or not such differences are biologically significant is a separate question reserved for the judgment of biologists.
Most biologists, even those leery of statistics, are generally aware that the venerable t-test (a.k.a., Student's t-test)14 is the standard method used to address questions related to differences between two sample means. Several factors influence the power of the t-test to detect significant differences. These include the size of the sample and the amount of variation present within the sample. If these sound familiar, they should. They were both factors that influence the size of the SEM, discussed in the preceding section. This is not a coincidence, as the heart of a t-test resides in estimating the standard error of the difference between two means (SEDM). Greater variance in the sample data increases the size of the SEDM, whereas higher sample sizes reduce it. Thus, lower variance and larger samples make it easier to detect differences. If the size of the SEDM is small relative to the absolute difference in means, then the finding will likely hold up as being statistically significant.
In fact, it is not necessary to deal directly with the SEDM to be perfectly proficient at interpreting results from a t-test. We will therefore focus primarily on aspects of the t-test that are most relevant to experimentalists. These include choices of carrying out tests that are either one- or two-tailed and are either paired or unpaired, assumptions of equal variance or not, and issues related to sample sizes and normality. We would also note, in passing, that alternatives to the t-test do exist. These tests, which include the computationally intensive bootstrap (see Section 6.7), typically require somewhat fewer assumptions than the t-test and will generally yield similar or superior results. For reasonably large sample sizes, a t-test will provide virtually the same answer and is currently more straightforward to carry out using available software and websites. It is also the method most familiar to reviewers, who may be skeptical of approaches that are less commonly used.
To aid in understanding the logic behind the t-test, as well as the basic requirements for the t-test to be valid, we need to introduce a few more statistical concepts. We will do this through an example. Imagine that we are interested in knowing whether or not the expression of gene a is altered in comma-stage embryos when gene b has been inactivated by a mutation. To look for an effect, we take total fluorescence intensity measurements15 of an integrated a::GFP reporter in comma-stage embryos in both wild-type (Control, Figure 5A) and b mutant (Test, Figure 5B) strains. For each condition, we analyze 55 embryos. Expression of gene a appears to be greater in the control setting; the difference between the two sample means is 11.3 billion fluorescence units (henceforth simply referred to as “11.3 units”).
Along with the familiar mean and SD, Figure 5 shows some additional information about the two data sets. Recall that in Section 1.2, we described what a data set looks like that is normally distributed (Figure 1). What we didn't mention is that distribution of the data16 can have a strong impact, at least indirectly, on whether or not a given statistical test will be valid. Such is the case for the t-test. Looking at Figure 5, we can see that the datasets are in fact a bit lopsided, having somewhat longer tails on the right. In technical terms, these distributions would be categorized as skewed right. Furthermore, because our sample size was sufficiently large (n=55), we can conclude that the populations from whence the data came are also skewed right. Although not critical to our present discussion, several parameters are typically used to quantify the shape of the data including the extent to which the data deviate from normality (e.g., skewness17, kurtosis18 and A-squared19). In any case, an obvious question now becomes, how can you know whether your data are distributed normally (or at least normally enough), to run a t-test?
Before addressing this question, we must first grapple with a bit of statistical theory. The Gaussian curve shown in Figure 6A represents a theoretical distribution of differences between sample means for our experiment. Put another way, this is the distribution of differences that we would expect to obtain if we were to repeat our experiment an infinite number of times. Remember that for any given population, when we randomly “choose” a sample, each repetition will generate a slightly different sample mean. Thus, if we carried out such sampling repetitions with our two populations ad infinitum, the bell-shaped distribution of differences between the two means would be generated (Figure 6A). Note that this theoretical distribution of differences is based on our actual sample means and SDs, as well as on the assumption that our original data sets were derived from populations that are normal, which is something we already know isn't true. So what to do?
Figure 6. Theoretical and simulated sampling distribution of differences between two means. The distributions are from the gene expression example. The mean and SE (SEDM) of the theoretical (A) and simulated (B) distributions are both approximately 11.3 and 1.4 units, respectively. The black vertical line in each panel is centered on the mean of the differences. The blue vertical lines indicate SEs (SEDMs) on each side.
As it happens, this lack of normality in the distribution of the populations from which we derive our samples does not often pose a problem. The reason is that the distribution of sample means, as well as the distribution of differences between two independent sample means (along with many20 other conventionally used statistics), is often normal enough for the statistics to still be valid. The reason is the The Central Limit Theorem, a “statistical law of gravity”, that states (in its simplest form21) that the distribution of a sample mean will be approximately normal providing the sample size is sufficiently large. How large is large enough? That depends on the distribution of the data values in the population from which the sample came. The more non-normal it is (usually, that means the more skewed), the larger the sample size requirement. Assessing this is a matter of judgment22. Figure 7 was derived using a computational sampling approach to illustrate the effect of sample size on the distribution of the sample mean. In this case, the sample was derived from a population that is sharply skewed right, a common feature of many biological systems where negative values are not encountered (Figure 7A). As can be seen, with a sample size of only 15 (Figure 7B), the distribution of the mean is still skewed right, although much less so than the original population. By the time we have sample sizes of 30 or 60 (Figure 7C, D), however, the distribution of the mean is indeed very close to being symmetrical (i.e., normal).
Figure 7. Illustration of Central Limit Theorem for a skewed population of values. Panel A shows the population (highly skewed right and truncated at zero); Panels B, C, and D show distributions of the mean for sample sizes of 15, 30, and 60, respectively, as obtained through a computational sampling approach. As indicated by the x axes, the sample means are approximately 3. The y axes indicate the number of computational samples obtained for a given mean value. As would be expected, larger-sized samples give distributions that are closer to normal and have a narrower range of values.
The Central Limit Theorem having come to our rescue, we can now set aside the caveat that the populations shown in Figure 5 are non-normal and proceed with our analysis. From Figure 6 we can see that the center of the theoretical distribution (black line) is 11.29, which is the actual difference we observed in our experiment. Furthermore, we can see that on either side of this center point, there is a decreasing likelihood that substantially higher or lower values will be observed. The vertical blue lines show the positions of one and two SDs from the apex of the curve, which in this case could also be referred to as SEDMs. As with other SDs, roughly 95% of the area under the curve is contained within two SDs. This means that in 95 out of 100 experiments, we would expect to obtain differences of means that were between “8.5” and “14.0” fluorescence units. In fact, this statement amounts to a 95% CI for the difference between the means, which is a useful measure and amenable to straightforward interpretation. Moreover, because the 95% CI of the difference in means does not include zero, this implies that the P-value for the difference must be less than 0.05 (i.e., that the null hypothesis of no difference in means is not true). Conversely, had the 95% CI included zero, then we would already know that the P-value will not support conclusions of a difference based on the conventional cutoff (assuming application of the two-tailed t-test; see below).
The key is to understand that the t-test is based on the theoretical distribution shown in Figure 6A, as are many other statistical parameters including 95% CIs of the mean. Thus, for the t-test to be valid, the shape of the actual differences in sample means must come reasonably close to approximating a normal curve. But how can we know what this distribution would look like without repeating our experiment hundreds or thousands of times? To address this question, we have generated a complementary distribution shown in Figure 6B. In contrast to Figure 6A, Figure 6B was generated using a computational re-sampling method known as bootstrapping (discussed in Section 6.7). It shows a histogram of the differences in means obtained by carrying out 1,000 in silico repeats of our experiment. Importantly, because this histogram was generated using our actual sample data, it automatically takes skewing effects into account. Notice that the data from this histogram closely approximate a normal curve and that the values obtained for the mean and SDs are virtually identical to those obtained using the theoretical distribution in Figure 6A. What this tells us is that even though the sample data were indeed somewhat skewed, a t-test will still give a legitimate result. Moreover, from this exercise we can see that with a sufficient sample size, the t-test is quite robust to some degree of non-normality in the underlying population distributions. Issues related to normality are also discussed further below.
Although t-tests always evaluate differences between two means, in some cases only one of the two mean values may be derived from an experimental sample. For example, we may wish to compare the number of vulval cell fates induced in wild-type hermaphrodites versus mutant m. Because it is broadly accepted that wild type induces (on average) three progenitor vulval cells, we could theoretically dispense with re-measuring this established value and instead measure it only in the mutant m background (Sulston and Horvitz, 1977). In such cases, we would be obliged to run a one-sample t-test to determine if the mean value of mutant m is different from that of wild type.
There is, however, a problem in using the one-sample approach, which is not statistical but experimental. Namely, there is always the possibility that something about the growth conditions, experimental execution, or alignment of the planets, could result in a value for wild type that is different from that of the established norm. If so, these effects would likely conspire to produce a value for mutant m that is different from the traditional wild-type value, even if no real difference exists. This could then lead to a false conclusion of a difference between wild type and mutant m. In other words, the statistical test, though valid, would be carried out using flawed data. For this reason, one doesn't often see one-sample t-tests in the worm literature. Rather, researchers tend to carry out parallel experiments on both populations to avoid being misled. Typically, this is only a minor inconvenience and provides much greater assurance that any conclusions will be legitimate. Along these lines, historical controls, including those carried out by the same lab but at different times, should typically be avoided.
One aspect of the t-test that tends to agitate users is the obligation to choose either the one or two-tailed versions of the test. That the term “tails” is not particularly informative only exacerbates the matter. The key difference between the one- and two-tailed versions comes down to the formal statistical question being posed. Namely, the difference lies in the wording of the research question. To illustrate this point, we will start by applying a two-tailed t-test to our example of embryonic GFP expression. In this situation, our typical goal as scientists would be to detect a difference between the two means. This aspiration can be more formally stated in the form of a research or alternative hypothesis. Namely, that the average expression levels of a::GFP in wild type and in mutant b are different. The null hypothesis must convey the opposite sentiment. For the two-tailed t-test, the null hypothesis is simply that the expression of a::GFP in wild type and mutant b backgrounds is the same. Alternatively, one could state that the difference in expression levels between wild type and mutant b is zero.
It turns out that our example, while real and useful for illustrating the idea that the sampling distribution of the mean can be approximately normal (and indeed should be if a t-test is to be carried out), even if the distribution of the data are not, is not so useful for illustrating P-value concepts. Hence, we will continue this discussion with a contrived variation: suppose the SEDM was 5.0, reflecting a very large amount of variation in the gene expression data. This would lead to the distribution shown in Figure 8A, which is analogous to the one from Figure 6A. You can see how the increase in the SEDM affects the values that are contained in the resulting 95% CI. The mean is still 11.3, but now there is some probability (albeit a small one) of obtaining a difference of zero, our null hypothesis. Figure 8B shows the same curve and SEDMs. This time, however, we have shifted the values of the x axis to consider the condition under which the null hypothesis is true. Thus the postulated difference in this scenario is zero (at the peak of the curve).
Figure 8. Graphical representation of a two-tailed t-test. (A) The same theoretical sampling distribution shown in Figure 6A in which the SEDM has been changed to 5.0 units (instead of 1.4). The numerical values on the x-axis represent differences from the mean in original units; numbers on the green background are values corresponding to the black and blue vertical lines. The black vertical line indicates a mean difference of 11.3 units, the blue vertical lines show SEs (SEDMs). (B) The results shown in panel A are considered for the case where the null hypothesis is indeed true (i.e., the difference of the means is zero). The units on the x-axis represent differences from the mean in SEs (SEDMs). As for panel A, the numbers on the green background correspond to the original differences. The rejection cutoffs are indicated with red lines using ( = 0.05 (i.e., the red lines partition 5% of the total space under the curve on each tail. The blue vertical line indicates the actual difference observed. The dashed blue line indicates the negative value of the observed actual difference. In this case, the two-tailed P-value for the difference in means will be equal to the proportion of the volume under the curve that is isolated by the two blue lines in each tail.
Now recall that The P-value answers the following question: If the null hypothesis is true, what is the probability that chance sampling could have resulted in a difference in sample means at least as extreme as the one obtained? In our experiment, the difference in sample means was 11.3, where a::GFP showed lower expression in the mutant b background. However, to derive the P-value for the two-tailed t-test, we would need to include the following two possibilities, represented here in equation forms:
Most notably, with a two-tailed t-test we impose no bias as to the direction of the difference when carrying out the statistical analysis. Looking at Figure 8B, we can begin to see how the P-value is calculated. Depicted is a normal curve, with the observed difference represented by the vertical blue line located at 11.3 units (∼2.3 SEs). In addition, a dashed vertical blue line at −11.3 is also included. Red lines are located at about 2 SEs to either side of the apex. Based on our understanding of the normal curve, we know that about 95% of the total area under the curve resides between the two red lines, leaving the remaining 5% to be split between the two areas outside of the red lines in the tail regions. Furthermore, the proportion of the area under the curve that is to the outside of each individual blue line is 1.3%, for a total of 2.6%. This directly corresponds to the calculated two-tailed P-value of 0.026. Thus, the probability of having observed an effect this large by mere chance is only 2.6%, and we can conclude that the observed difference of 11.3 is statistically significant.
Once you understand the idea behind the two-tailed t-test, the one-tailed type is fairly straightforward. For the one-tailed t-test, however, there will always be two distinct versions, each with a different research hypothesis and corresponding null hypothesis. For example, if there is sufficient a priori23 reason to believe that GFPwt will be greater than GFPmut b, then the research hypothesis could be written as
This means that the null hypothesis would be written as
Most importantly, the P-value for this test will answer the question: If the null hypothesis is true, what is the probability that the following result could have occurred by chance sampling?
Looking at Figure 8B, we can see that the answer is just the proportion of the area under the curve that lies to the right of positive 11.3 (solid vertical blue line). Because the graph is perfectly symmetrical, the P-value for this right-tailed test will be exactly half the value that we determined for the two-tailed test, or 0.013. Thus in cases where the direction of the difference coincides with a directional research hypothesis, the P-value of the one-tailed test will always be half that of the two-tailed test. This is a useful piece of information. Anytime you see a P-value from a one-tailed t-test and want to know what the two-tailed value would be, simply multiply by two.
Alternatively, had there been sufficient reason to posit a priori that GFPmut b will be greater than GFPwt, and then the research hypothesis could be written as
Of course, our experimental result that GFPwt was greater than GFPmut b clearly fails to support this research hypothesis. In such cases, there would be no reason to proceed further with a t-test, as the P-value in such situations is guaranteed to be >0.5. Nevertheless, for the sake of completeness, we can write out the null hypothesis as
And the P-value will answer the question: If the null hypothesis is true, what is the probability that the following result could have occurred by chance sampling?
Or, written slightly differently to keep things consistent with Figure 8B,
This one-tailed test yields a P-value of 0.987, meaning that the observed lower mean of a::GFP in mut b embryos is entirely consistent with a null hypothesis of GFPmut b ≤ GFPwt.
Interestingly, there is considerable debate, even among statisticians, regarding the appropriate use of one- versus two-tailed t-tests. Some argue that because in reality no two population means are ever identical, that all tests should be one tailed, as one mean must in fact be larger (or smaller) than the other (Jones and Tukey, 2000). Put another way, the null hypothesis of a two-tailed test is always a false premise. Others encourage standard use of the two-tailed test largely on the basis of its being more conservative. Namely, the P-value will always be higher, and therefore fewer false-positive results will be reported. In addition, two-tailed tests impose no preconceived bias as to the direction of the change, which in some cases could be arbitrary or based on a misconception. A universally held rule is that one should never make the choice of a one-tailed t-test post hoc24 after determining which direction is suggested by your data. In other words, if you are hoping to see a difference and your two-tailed P-value is 0.06, don't then decide that you really intended to do a one-tailed test to reduce the P-value to 0.03. Alternatively, if you were hoping for no significant difference, choosing the one-tailed test that happens to give you the highest P-value is an equally unacceptable practice.
Generally speaking, one-tailed tests are often reserved for situations where a clear directional outcome is anticipated or where changes in only one direction are relevant to the goals of the study. Examples of the latter are perhaps more often encountered in industry settings, such as testing a drug for the alleviation of symptoms. In this case, there is no reason to be interested in proving that a drug worsens symptoms, only that it improves them. In such situations, a one-tailed test may be suitable. Another example would be tracing the population of an endangered species over time, where the anticipated direction is clear and where the cost of being too conservative in the interpretation of data could lead to extinction. Notably, for the field of C. elegans experimental biology, these circumstances rarely, if ever, arise. In part for this reason, two-tailed tests are more common and further serve to dispel any suggestion that one has manipulated the test to obtain a desired outcome.
It is common to read in textbooks that one of the underlying assumptions of the t-test is that both samples should be derived from populations of equal variance. Obviously this will often not be the case. Furthermore, when using the t-test, we are typically not asking whether or not the samples were derived from identical populations, as we already know they are not. Rather, we want to know if the two independent populations from which they were derived have different means. In fact, the original version of the t-test, which does not formally take into account unequal sample variances, is nevertheless quite robust for small or even moderate differences in variance. Nevertheless, it is now standard to use a modified version of the t-test that directly adjusts for unequal variances. In most statistical programs, this may simply require checking or unchecking a box. The end result is that for samples that do have similar variances, effectively no differences in P-values will be observed between the two methods. For samples that do differ considerably in their variances, P-values will be higher using the version that takes unequal variances into account. This method therefore provides a slightly more conservative and accurate estimate for P-values and can generally be recommended.
Also, just to reinforce a point raised earlier, greater variance in the sample data will lead to higher P-values because of the effect of sample variance on the SEDM. This will make it more difficult to detect differences between sample means using the t-test. Even without any technical explanation, this makes intuitive sense given that greater scatter in the data will create a level of background noise that could obscure potential differences. This is particularly true if the differences in means are small relative to the amount of scatter. This can be compensated for to some extent by increasing the sample size. This, however, may not be practical in some cases, and there can be downsides associated with accumulating data solely for the purpose of obtaining low P-values (see Section 6.3).
Technically speaking, we know that for t-tests to be valid, the distribution of the differences in means must be close to normal (discussed above). For this to be the case, the populations from which the samples are derived must also be sufficiently close to normal. Of course we seldom know the true nature of populations and can only infer this from our sample data. Thus in practical terms the question often boils down to whether or not the sample data suggest that the underlying population is normal or normal enough. The good news is that in cases where the sample size is not too small, the distribution of the sample will reasonably reflect the population from which it was derived (as mentioned above). The bad news is that with small sample sizes (say below 20), we may not be able to tell much about the population distribution. This creates a considerable conundrum when dealing with small samples from unknown populations. For example, for certain types of populations, such as a theoretical collection of bands on a western blot, we may have no way of knowing if the underlying population is normal or skewed and probably can't collect sufficient data to make an informed judgment. In these situations, you would admittedly use a t-test at your own risk25.
Textbooks will tell you that using highly skewed data for t-tests can lead to unreliable P-values. Furthermore, the reliability of certain other statistics, such as CIs, can also be affected by the distribution of data. In the case of the t-test, we know that the ultimate issue isn't whether the data or populations are skewed but whether the theoretical population of differences between the two means is skewed. In the examples shown earlier (Figures 6 and 8), the shapes of the distributions were normal, and thus the t-tests were valid, even though our original data were skewed (Figure 5). A basic rule of thumb is that if the data are normal or only slightly skewed, then the test statistic will be normal and the t-test results will be valid, even for small sample sizes. Conversely, if one or both samples (or populations) are strongly skewed, this can result in a skewed test statistic and thus invalid statistical conclusions.
Interestingly, although increasing the sample size will not change the underlying distribution of the population, it can often go a long way toward correcting for skewness in the test statistic26. Thus, the t-test often becomes valid, even with fairly skewed data, if the sample size is large enough. In fact, using data from Figure 5, we did a simulation study and determined that the sampling distribution for the difference in means is indeed approximately normal with a sample size of 30 (data not shown). In that case, the histogram of that sampling distribution looked very much like that in Figure 6B, with the exception that the SD27 of the distribution was ∼1.9 rather than 1.4. In contrast, carrying out a simulation with a sample size of only 15 did not yield a normal distribution of the test statistic and thus the t-test would not have been valid.
Unfortunately, there is no simple rule for choosing a minimum sample size to protect against skewed data, although some textbooks recommend 30. Even a sample size of 30, however, may not be sufficient to correct for skewness or kurtosis in the test statistic if the sample data (i.e., populations) are severely non-normal to begin with28. The bottom line is that there are unfortunately no hard and fast rules to rely on. Thus, if you have reason to suspect that your samples or the populations from which there are derived are strongly skewed, consider consulting your nearest statistician for advice on how to proceed. In the end, given a sufficient sample size, you may be cleared for the t-test. Alternatively, several classes of nonparametric tests can potentially be used (Section 6.5). Although these tests tend to be less powerful than the t-test at detecting differences, the statistical conclusions drawn from these approaches will be much more valid. Furthermore, the computationally intensive method bootstrapping retains the power of the t-test but doesn't require a normal distribution of the test statistic to yield valid results.
In some cases, it may also be reasonable to assume that the population distributions are normal enough. Normality, or something quite close to it, is typically found in situations where many small factors serve to contribute to the ultimate distribution of the population. Because such effects are frequently encountered in biological systems, many natural distributions may be normal enough with respect to the t-test. Another way around this conundrum is to simply ask a different question, one that doesn't require the t-test approach. In fact, the western blot example is one where many of us would intuitively look toward analyzing the ratios of band intensities within individual blots (discussed in Section 6.5).
You may be surprised to learn that nothing can stop you from running a t-test with sample sizes of two. Of course, you may find it difficult to convince anyone of the validity of your conclusion, but run it you may! Another problem is that very low sample sizes will render any test much less powerful. What this means in practical terms is that to detect a statistically significant difference with small sample sizes, the difference between the two means must be quite large. In cases where the inherent difference is not large enough to compensate for a low sample size, the P-value will likely be above the critical threshold. In this event, you might state that there is insufficient evidence to indicate a difference between the populations, although there could be a difference that the experiment failed to detect. Alternatively, it may be tempting to continue gathering samples to push the P-value below the traditionally acceptable threshold of 0.05. As to whether this is a scientifically appropriate course of action is a matter of some debate, although in some circumstances it may be acceptable. However, this general tactic does have some grave pitfalls, which are addressed in later sections (e.g., Section 6.3).
One good thing about working with C. elegans, however, is that for many kinds of experiments, we can obtain fairly large sample sizes without much trouble or expense. The same cannot be said for many other biological or experimental systems. This advantage should theoretically allow us to determine if our data are normal enough or to simply not care about normality since our sample sizes are high. In any event, we should always strive to take advantage of this aspect of our system and not short-change our experiments. Of course, no matter what your experimental system might be, issues such as convenience and expense should not be principal driving forces behind the determination of sample size. Rather, these decisions should be based on logical, pragmatic, and statistically informed arguments (see Section 6.2 on power analysis).
Nevertheless, there are certain kinds of common experiments, such as qRT-PCR, where a sample size of three is quite typical. Of course, by three we do not mean three worms. For each sample in a qRT-PCR experiment, many thousands of worms may have been used to generate a single mRNA extract. Here, three refers to the number of biological replicates. In such cases, it is generally understood that worms for the three extracts may have been grown in parallel but were processed for mRNA isolation and cDNA synthesis separately. Better yet, the templates for each biological replicate may have been grown and processed at different times. In addition, qRT-PCR experiments typically require technical replicates. Here, three or more equal-sized aliquots of cDNA from the same biological replicate are used as the template in individual PCR reactions. Of course, the data from technical replicates will nearly always show less variation than data from true biological replicates. Importantly, technical replicates should never be confused with biological replicates. In the case of qRT-PCR, the former are only informative as to the variation introduced by the pipetting or amplification process. As such, technical replicates should be averaged, and this value treated as a single data point.
In this case, suppose for the sake of discussion that each replicate contains extracts from 5,000 worms. If all 15,000 worms can be considered to be from some a single population (at least with respect to the mRNA of interest), then each observed value is akin to a mean from a sample of 5,000. In that case, one could likely argue that the three values do come from a normal population (the Central Limit Theorem having done its magic on each), and so a t-test using the mean of those three values would be acceptable from a statistical standpoint. It might possibly still suffer from a lack of power, but the test itself would be valid. Similarly, western blot quantitation values, which average proteins from many thousands of worms, could also be argued to fall under this umbrella.
The paired t-test is a powerful way to detect differences in two sample means, provided that your experiment has been designed to take advantage of this approach. In our example of embryonic GFP expression, the two samples were independent in that the expression within any individual embryo was not linked to the expression in any other embryo. For situations involving independent samples, the paired t-test is not applicable; we carried out an unpaired t-test instead. For the paired method to be valid, data points must be linked in a meaningful way. If you remember from our first example, worms that have a mutation in b show lower expression of the a::GFP reporter. In this example of a paired t-test, consider a strain that carries a construct encoding a hairpin dsRNA corresponding to gene b. Using a specific promoter and the appropriate genetic background, the dsRNA will be expressed only in the rightmost cell of one particular neuronal pair, where it is expected to inhibit the expression of gene b via the RNAi response. In contrast, the neuron on the left should be unaffected. In addition, this strain carries the same a::GFP reporter described above, and it is known that this reporter is expressed in both the left and right neurons at identical levels in wild type. The experimental hypothesis is therefore that, analogous to what was observed in embryos, fluorescence of the a::GFP reporter will be weaker in the right neuron, where gene b has been inhibited.
In this scenario, the data are meaningfully paired in that we are measuring GFP levels in two distinct cells, but within a single worm. We then collect fluorescence data from 14 wild-type worms and 14 b(RNAi) worms. A visual display of the data suggests that expression of a::GFP is perhaps slightly decreased in the right cell where gene b has been inhibited, but the difference between the control and experimental dataset is not very impressive (Figure 9A, B). Furthermore, whereas the means of GFP expression in the left neurons in wild-type and b(RNAi) worms are nearly identical, the mean of GFP expression in the right neurons in wild type is a bit higher than that in the right neurons of b(RNAi) worms. For our t-test analysis, one option would be to ignore the natural pairing in the data and treat left and right cells of individual animals as independent. In doing so, however, we would hinder our ability to detect real differences. The reason is as follows. We already know that GFP expression in some worms will happen to be weaker or stronger (resulting in a dimmer or brighter signal) than in other worms. This variability, along with a relatively small mean difference in expression, may preclude our ability to support differences statistically. In fact, a two-tailed t-test using the (hypothetical) data for right cells from wild-type and b(RNAi) strains (Figure 9B) turns out to give a P > 0.05.
Figure 9C, D, in contrast, shows a slightly different arrangement of the same GFP data. Here the wild-type and b(RNAi) strains have been separated, and we are specifically comparing expression in the left and right neurons for each genotype. In addition, lines have been drawn between left and right data points from the same animal. Two things are quite striking. One is that worms that are bright in one cell tend to be bright in the other. Second, looking at b(RNAi) worms, we can see that within individuals, there is a strong tendency to have reduced expression in the right neuron as compared with its left counterpart (Figure 9D). However, because of the inherent variability between worms, this difference was largely obscured when we failed to make use of the paired nature of the experiment. This wasn't a problem in the embryonic analysis, because the difference between wild type and b mutants was large enough relative to the variability between embryos. In the case of neurons (and the use of RNAi), the difference was, however, much smaller and thus fell below the level necessary for statistical validation. Using a paired two-tailed t-test for this dataset gives a P < 0.01.
The rationale behind using the paired t-test is that it takes meaningfully linked data into account when calculating the P-value. The paired t-test works by first calculating the difference between each individual pair. Then a mean and variance are calculated for all the differences among the pairs. Finally, a one-sample t-test is carried out where the null hypothesis is that the mean of the differences is equal to zero. Furthermore, the paired t-test can be one- or two-tailed, and arguments for either are similar to those for two independent means. Of course, standard programs will do all of this for you, so the inner workings are effectively invisible. Given the enhanced power of the paired t-test to detect differences, it is often worth considering how the statistical analysis will be carried out at the stage when you are developing your experimental design. Then, if it's feasible, you can design the experiment to take advantage of the paired t-test method.
Some textbooks, particularly older ones, present a method known as the critical value approach in conjunction with the t-test. This method, which traditionally involves looking up t-values in lengthy appendices, was developed long before computer software was available to calculate precise P-values. Part of the reason this method may persist, at least in some textbooks, is that it provides authors with a vehicle to explain the basis of hypothesis testing along with certain technical aspects of the t-test. As a modern method for analyzing data, however, it has long since gone the way of the dinosaur. Feel no obligation to learn this.
13The term “statistically significant”, when applied to the results of a statistical test for a difference between two means, implies only that it is plausible that the observed difference (i.e., the difference that arises from the data) likely represents a difference that is real. It does not imply that the difference is “biologically significant” (i.e., important). A better phrase would be “statistically plausible” or perhaps “statistically supported”. Unfortunately, “statistically significant” (in use often shortened to just “significant”) is so heavily entrenched that it is unlikely we can unseat it. It's worth a try, though. Join us, won't you?
14When William Gossett introduced the test, it was in the context of his work for Guinness Brewery. To prevent the dissemination of trade secrets and/or to hide the fact that they employed statisticians, the company at that time had prohibited the publication of any articles by their employees. Gossett was allowed an exception, but the higher-ups insisted that he use a pseudonym. He chose the unlikely moniker “Student”.
15These are measured by the number of pixels showing fluorescence in a viewing area of a specified size. We will use “billions of pixels” as our unit of measurement.
16More accurately, it is the distribution of the underlying populations that we are really concerned with, although this can usually only be inferred from the sample data.
17For data sets with distributions that are perfectly symmetric, the skewness will be zero. In this case the mean and median of the data set are identical. For left-skewed distributions, the mean is less than the median and the skewness will be a negative number. For right-skewed distributions, the mean is more than the median and the skewness will be a positive number.
18Kurtosis describes the shape or “peakedness” of the data set. In the case of a normal distribution, this number is zero. Distributions with relatively sharp peaks and long tails will have a positive kurtosis value whereas distributions with relatively flat peaks and short tails will have a negative kurtosis value.
19A-squared (A2) refers to a numerical value produced by the Anderson-Darling test for normality. The test ultimately generates an approximate P-value where the null hypothesis is that the data are derived from a population that is normal. In the case of the data in Figure 5, the conclusion is that there is < 0.5% chance that the sample data were derived from a normal population. The conclusion of non-normality can also be reached informally by a visual inspection of the histograms. The Anderson-Darling test does not indicate whether test statistics generated by the sample data will be sufficiently normal.
20The list is long, but it includes coefficients in regression models and estimated binomial proportions (and differences in proportions from two independent samples). For an illustration of this phenomenon for proportions, see Figure 12 and discussion thereof.
21There are actually many Central Limit Theorems, each with the same conclusion: normality prevails for the distribution of the statistic under consideration. Why many? This is so mainly because details of the proof of the theorem depend on the particular statistical context.
22And, as we all know, good judgment comes from experience, and experience comes from bad judgment.
23Meaning reasons based on prior experience.
24Meaning “after the fact”.
25Also see discussion on sample sizes (Section 2.7) and Section 5 for a more complete discussion of issues related to western blots.
26This is due to a statistical “law of gravity” called the Central Limit Theorem: as the sample size gets larger, the distribution of the sample mean (i.e., the distribution you would get if you repeated the study ad infinitum) becomes more and more like a normal distribution.
27Estimated from the data; again, this is also called the SEDM.
28In contrast, you can, with data from sample sizes that are not too small, ask whether they (the data and, hence, the population from whence they came) are normal enough. Judging this requires experience, but, in essence, the larger the sample size, the less normal the distribution can be without causing much concern.
The two-sample t-test works well in situations where we need to determine if differences exist between two populations for which we have sample means. But what happens when our analyses involve comparisons between three or more separate populations? Here things can get a bit tricky. Such scenarios tend to arise in one of several ways. Most common to our field is that we have obtained a collection of sample means that we want to compare with a single standard. For example, we might measure the body lengths of young adult-stage worms grown on RNAi-feeding plates, each targeting one of 100 different collagen genes. In this case, we would want to compare mean lengths from animals grown on each plate with a control RNAi that is known to have no effect on body length. On the surface, the statistical analysis might seem simple: just carry out 100 two-sample t-tests where the average length from each collagen RNAi plate is compared with the same control. The problem with this approach is the unavoidable presence of false-positive findings (also known as Type I errors). The more t-tests you run, the greater the chance of obtaining a statistically significant result through chance sampling. Even if all the populations were identical in their lengths, 100 t-tests would result on average in five RNAi clones showing differences supported by P-values of <0.05, including one clone with a P-value of <0.01. This type of multiple comparisons problem is common in many of our studies and is a particularly prevalent issue in high-throughput experiments such as microarrays, which typically involve many thousands of comparisons.
Taking a slightly different angle, we can calculate the probability of incurring at least one false significance in situations of multiple comparisons. For example, with just two t-tests and a significance threshold of 0.05, there would be an ∼10% chance29 that we would obtain at least one P-value that was <0.05 just by chance [1 – (0.95)2 = 0.0975]. With just fourteen comparisons, that probability leaps to >50% (1 – (0.95)14 = 0.512). With 100 comparisons, there is a 99% chance of obtaining at least one statistically significant result by chance. Using probability calculators available on the web (also see Section 4.10), we can determine that for 100 tests there is a 56.4% chance of obtaining five or more false positives and a 2.8% chance of obtaining ten or more. Thinking about it this way, we might be justifiably concerned that our studies may be riddled with incorrect conclusions! Furthermore, reducing the chosen significance threshold to 0.01 will only help so much. In this case, with 50 comparisons, there is still an ∼40% probability that at least one comparison will sneak below the cutoff by chance. Moreover, by reducing our threshold, we run the risk of discarding results that are both statistically and biologically significant.
A related but distinct situation occurs when we have a collection of sample means, but rather than comparing each of them to a single standard, we want to compare all of them to each other. As is with the case of multiple comparisons to a single control, the problem lies in the sheer number of tests required. With only five different sample means, we would need to carry out 10 individual t-tests to analyze all possible pair-wise comparisons [5(5 − 1)/2 = 10]. With 100 sample means, that number skyrockets to 4,950. (100(100 − 1)/2 = 4,950). Based on a significance threshold of 0.05, this would lead to about 248 statistically significant results occurring by mere chance! Obviously, both common sense, as well as the use of specialized statistical methods, will come into play when dealing with these kinds of scenarios. In the sections below, we discuss some of the underlying concepts and describe several practical approaches for handling the analysis of multiple means.
Before delving into some of the common approaches used to cope with multiple comparisons, it is worth considering an experimental scenario that would likely not require specialized statistical methods. Specifically, we may consider the case of a large-scale “functional genomics screen”. In C. elegans, these would typically be carried out using RNAi-feeding libraries (Kamath et al., 2003) or chemical genetics (Carroll et al., 2003) and may involve many thousands of comparisons. For example, if 36 RNAi clones are ultimately identified that lead to resistance to a particular bacterial pathogen from a set of 17,000 clones tested, how does one analyze this result? No worries: the methodology is not composed of 17,000 statistical tests (each with some chance of failing). That's because the final reported tally, 36 clones, was presumably not the result of a single round of screening. In the first round (the primary screen), a larger number (say, 200 clones) might initially be identified as possibly resistant (with some “false significances” therein). A second or third round of screening would effectively eliminate virtually all of the false positives, reducing the number of clones that show a consistent biological affect to 36. In other words, secondary and tertiary screening would reduce to near zero the chance that any of the clones on the final list are in error because the chance of getting the same false positives repeatedly would be very slim. This idea of “safety through independent experimental repeats” is also addressed in Section 4.10 in the context of proportion data. Perhaps more than anything else, carrying out independent repeats is often best way to solidify results and avoid the presence of false positives within a dataset.
To help grapple with the problems inherent to multiple comparisons, statisticians came up with something called the family-wise error rate. This is also sometimes referred to as the family-wide error rate, which may provide a better description of the underlying intent. The basic idea is that rather than just considering each comparison in isolation, a statistical cutoff is applied that takes into account the entire collection of comparisons. Recall that in the case of individual comparisons (sometimes called the per-comparison or comparison-wise error rate), a P-value of <0.05 tells us that for that particular comparison, there is less than a 5% chance of having obtained a difference at least as large as the one observed by chance. Put another way, in the absence of any real difference between two populations, there is a 95% chance that we will not render a false conclusion of statistical significance. In the family-wise error rate approach, the criterion used to judge the statistical significance of any individual comparison is made more stringent as a way to compensate for the total number of comparisons being made. This is generally done by lowering the P-value cutoff (α level) for individual t-tests. When all is said and done, a P-value of <0.05 will mean that there is less than a 5% chance that the entire collection of declared positive findings contains any false positives.
We can use our example of the collagen experiment to further illustrate the meaning of the family-wise error rate. Suppose we test 100 genes and apply a family-wise error rate cutoff of 0.05. Perhaps this leaves us with a list of 12 genes that lead to changes in body size that are deemed statistically significant. This means that there is only a 5% chance that one or more of the 12 genes identified is a false positive. This also means that if none of the 100 genes really controlled body size, then 95% of the time our experiment would lead to no positive findings. Without this kind of adjustment, and using an α level of 0.05 for individual tests, the presence of one or more false positives in a data set based on 100 comparisons could be expected to happen >99% of the time. Several techniques for applying the family-wise error rate are described below.
The Bonferroni method, along with several related techniques, is conceptually straightforward and provides conservative family-wise error rates. To use the Bonferroni method, one simply divides the chosen family-wise error rate (e.g., 0.05) by the number of comparisons to obtain a Bonferroni-adjusted P-value cutoff. Going back to our example of the collagen genes, if the desired family-wise error rate is 0.05 and the number of comparisons is 100, the adjusted per-comparison significance threshold would be reduced to 0.05/100 = 0.0005. Thus, individual t-tests yielding P-values as low as 0.0006 would be declared insignificant. This may sound rather severe. In fact, a real problem with the Bonferroni method is that for large numbers of comparisons, the significance threshold may be so low that one may fail to detect a substantial proportion of true positives within a data set. For this reason, the Bonferroni method is widely considered to be too conservative in situations with large numbers of comparisons.
Another variation on the Bonferroni method is to apply significance thresholds for each comparison in a non-uniform manner. For example, with a family-wise error rate of 0.05 and 10 comparisons, a uniform cutoff would require any given t-test to have an associated P-value of <0.005 to be declared significant. Another way to think about this is that the sum of the 10 individual cutoffs must add up to 0.05. Interestingly, the integrity of the family-wise error rate is not compromised if one were to apply a 0.04 significance threshold for one comparison, and a 0.00111 (0.01/9) significance threshold for the remaining nine. This is because 0.04 + 9(0.00111) ≈ 0.05. The rub, however, is that the decision to apply non-uniform significance cutoffs cannot be made post hoc based on how the numbers shake out! For this method to be properly implemented, researchers must first prioritize comparisons based on the perceived importance of specific tests, such as if a negative health or environmental consequence could result from failing to detect a particular difference. For example, it may be more important to detect a correlation between industrial emissions and childhood cancer rates than to effects on the rate of tomato ripening. This may all sound rather arbitrary, but it is nonetheless statistically valid.
As discussed above, the Bonferroni method runs into trouble in situations where many comparisons are being made because a substantial proportion of true positives are likely to be discarded for failing to score below the adjusted significance threshold. Stated another way, the power of the experiment to detect real differences may become unacceptably low. Benjamini and Hochberg (1995) are credited with introducing the idea of the false discovery rate (FDR), which has become an indispensable approach for handling the statistical analysis of experiments composed of large numbers of comparisons. Importantly, the FDR method has greater power than does the Bonferroni method. In the vernacular of the FDR method, a statistically significant finding is termed a “discovery”. Ultimately, the FDR approach allows the investigator to set an acceptable level of false discoveries (usually 5%), which means that any declared significant finding has a 5% chance of being a false positive. This differs fundamentally from the idea behind the family-wise model, where an error rate of 5% means that there is a 5% chance that any of the declared significant findings are false. The latter method starts from the position that no differences exist. The FDR method does not suppose this.
The FDR method is carried out by first making many pairwise comparisons and then ordering them according to their associated P-values, with lowest to highest displayed in a top to bottom manner. In the examples shown in Table 3, this was done with only 10 comparisons (for three different data sets), but this method is more commonly applied to studies involving hundreds or thousands of comparisons. What makes the FDR method conceptually unique is that each of the test-derived P-values is measured against a different significance threshold. In the example with 10 individual tests, the one giving the lowest P-value is measured against30 0.005 (0.05/10). Conversely, the highest P-value is measured against 0.05. With ten comparisons, the other significance thresholds simply play out in ordered increments of 0.005 (Table 3). For example, the five significance thresholds starting from the top of the list would be 0.005, 0.010, 0.015, 0.020, and 0.025. The formula is k(α/C), where C is the number of comparisons and k is the rank order (by sorted P-values) of the comparison. If 100 comparisons were being made, the highest threshold would still be 0.05, but the lowest five in order would be 0.0005, 0.0010, 0.0015, 0.0020, and 0.0025. Having paired off each experimentally derived P-value with a different significance threshold, one checks to see if the P-value is less than the prescribed threshold. If so, then the difference is declared to be statistically significant (a discovery), at which point one moves on to the next comparison, involving the second-lowest P-value. This process continues until a P-value is found that is higher than the corresponding threshold. At that point, this and all remaining results are deemed not significant.
Table 3. Illustration of FDR method, based on artificial P-values from 10 comparisons.
| Comparison | FDR Critical Value | P-values | ||
|---|---|---|---|---|
| Data Set #1 | Data Set #2 | Data Set #3 | ||
| 1 | 0.005 | 0.001* | 0.004* | 0.006 |
| 2 | 0.010 | 0.003* | 0.008* | 0.008 |
| 3 | 0.015 | 0.012* | 0.014* | 0.011 |
| 4 | 0.020 | 0.015* | 0.048 | 0.019 |
| 5 | 0.025 | 0.019* | 0.210 | 0.020 |
| 6 | 0.030 | 0.022* | 0.346 | 0.025 |
| 7 | 0.035 | 0.034* | 0.719 | 0.111 |
| 8 | 0.040 | 0.056 | 0.754 | 0.577 |
| 9 | 0.045 | 0.127 | 0.810 | 0.636 |
| 10 | 0.050 | 0.633 | 0.985 | 0.731 |
|
The highlighted values indicate the first P-value that is larger than the significance threshold (i.e., the FDR critical value)]. *Comparisons that were declared significant by the method. |
||||
Examples of how this can play out are shown in Table 3. Note that even though some of the comparisons below the first failed test may themselves be less than their corresponding significance thresholds (Data Set #3), these tests are nevertheless declared not significant. This may seem vexing, but without this property the test would not work. This is akin to a “one strike and you're out” rule. Put another way, that test, along with all those below it on the list, are declared persona non grata and asked to leave the premises!
Although the FDR approach is not hugely intuitive, and indeed the logic is not easily tractable, it is worth considering several scenarios to see how the FDR method might play out. For example, with 100 independent tests of two populations that are identical, chance sampling would be expected to result on average with a single t-test having an associated P-value of 0.0131. However, given that the corresponding significance threshold would be 0.0005, this test would not pass muster and the remaining tests would also be thrown out. Even if by chance a P-value of <0.0005 was obtained, the next likely lowest P-value on the list, 0.02, would be measured against 0.001, underscoring that the FDR method will be effective at weeding out imposters. Next, consider the converse situation: 100 t-tests carried out on two populations that are indeed different. Furthermore, based on the magnitude of the difference and the chosen sample size, we would expect to obtain an average P-value of 0.01 for all the tests. Of course, chance sampling will lead to some experimental differences that result in P-values that are higher or lower than 0.01, including on average one that is 0.0001 (0.01/100). Because this is less than the cutoff of 0.0005, this would be classified as a discovery, as will many, though not all, of the tests on this particular list. Thus, the FDR approach will also render its share of false-negative conclusions (often referred to as Type II errors). But compared with the Bonferroni method, where the significance threshold always corresponds to the lowest FDR cutoff, the proportion of these errors will be much smaller.
Entire books are devoted to the statistical method known as analysis of variance32 (ANOVA). This section will contain only three paragraphs. This is in part because of the view of some statisticians that ANOVA techniques are somewhat dated or at least redundant with other methods such as multiple regression (see Section 5.5). In addition, a casual perusal of the worm literature will uncover relatively scant use of this method. Traditionally, an ANOVA answers the following question: are any of the mean values within a dataset likely to be derived from populations33 that are truly different? Correspondingly, the null hypothesis for an ANOVA is that all of the samples are derived from populations, whose means are identical and that any difference in their means are due to chance sampling. Thus, an ANOVA will implicitly compare all possible pairwise combinations of samples to each other in its search for differences. Notably, in the case of a positive finding, an ANOVA will not directly indicate which of the populations are different from each other. An ANOVA tells us only that at least one sample is likely to be derived from a population that is different from at least one other population.
Because such information may be less than totally satisfying, an ANOVA is often used in a two-tiered fashion with other tests; these latter tests are sometimes referred to as post hoc tests. In cases where an ANOVA suggests the presence of different populations, t-tests or other procedures (described below) can be used to identify differences between specific populations. Moreover, so long as the P-value associated with the ANOVA is below the chosen significance threshold, the two means that differ by the greatest amount are assured of being supported by further tests. The correlate, however, is not true. Namely, it is possible to “cherry pick” two means from a data set (e.g., those that differ by the greatest amount) and obtain a P value that is <0.05 based on a t-test even if the P-value of the ANOVA (which simultaneously takes into account all of the means) is >0.05. Thus, ANOVA will provide a more conservative interpretation than t-tests using chosen pairs of means. Of course, focusing on certain comparisons may be perfectly valid in some instances (see discussion of planned comparisons below). In fact, it is generally only in situations where there is insufficient structure among treatment groups to inspire particular comparisons where ANOVA is most applicable. In such cases, an insignificant ANOVA finding might indeed be grounds for proceeding no further.
In cases of a positive ANOVA finding, a commonly used post hoc method is Tukey's test, which goes by a number of different names including Tukey's honest significant difference test and the Tukey-Kramer test. The output of this test is a list of 95% CIs of the differences between means for all possible pairs of populations. Real differences between populations are indicated when the 95% CI for a given comparison does not include zero. Moreover, because of the family-wise nature of this analysis, the entire set of comparisons has only a 5% chance of containing any false positives. As is the case for other methods for multiple comparisons, the chance of obtaining false negatives increases with the number of populations being tested, and, with post hoc ANOVA methods, this increase is typically exponential. For Tukey's test, the effect of increasing the number of populations is manifest as a widening of 95% CIs, such that a higher proportion will encompass zero. Tukey's test does have more power than the Bonferroni method but does not generate precise P-values for specific comparisons. To get some idea of significance levels, however, one can run Tukey's test using several different family-wise significance thresholds (0.05, 0.01, etc.) to see which comparisons are significant at different thresholds. In addition to Tukey's test, many other methods have been developed for post hoc ANOVA including Dunnett's test, Holm's test, and Scheffe's test. Thus if your analyses take you heavily into the realm of the ANOVA, it may be necessary to educate yourself about the differences between these approaches.
Figure 10 provides a visual summary of the multiple comparisons methods discussed above. As can be seen, the likelihood of falsely declaring a result to be statistically significant is highest when conducting multiple t-tests without corrections and lowest using Bonferroni-type methods. Conversely, incorrectly concluding no significant difference even when one exists is most likely to occur using the Bonferroni method. Thus the Bonferroni method is the most conservative of the approaches discussed, with FDR occupying the middle ground. Additionally, there is no rule as to whether the uniform or non-uniform Bonferroni method will be more conservative as this will always be situation dependent. Though discussed above, ANOVA has been omitted from Figure 10 since this method does not apply to individual comparisons. Nevertheless, it can be posited that ANOVA is more conservative than uncorrected multiple t-tests and less conservative than Bonferroni methods. Finally, we can note that the statistical power of an analysis is lowest when using approaches that are more conservative (discussed further in Section 6.2).
There is no law that states that all possible comparisons must be made. It is perfectly permissible to choose a small subset of the comparisons for analysis, provided that this decision is made prior to generating the data and not afterwards based on how the results have played out! In addition, with certain datasets, only certain comparisons may make biological sense or be of interest. Thus one can often focus on a subset of relevant comparisons. As always, common sense and a clear understanding of the biology is essential. These situations are sometimes referred to as planned comparisons, thus emphasizing the requisite premeditation. An example might be testing for the effect on longevity of a particular gene that you have reason to believe controls this process. In addition, you may include some negative controls as well as some “long-shot” candidates that you deduced from reading the literature. The fact that you included all of these conditions in the same experimental run, however, would not necessarily obligate you to compensate for multiple comparisons when analyzing your data.
In addition, when the results of multiple tests are internally consistent, multiple comparison adjustments are often not needed. For example, if you are testing the ability of gene X loss of function to suppress a gain-of-function mutation in gene Y, you may want to test multiple mutant alleles of gene X as well as RNAi targeting several different regions of X. In such cases, you may observe varying degrees of genetic suppression under all the tested conditions. Here you need not adjust for the number of tests carried out, as all the data are supporting the same conclusion. In the same vein, it could be argued that suppression of a mutant phenotype by multiple genes within a single pathway or complex could be exempt from issues of multiple comparisons. Finally, as discussed above, carrying out multiple independent tests may be sufficient to avoid having to apply statistical corrections for multiple comparisons.
Imagine that you have written up a manuscript that contains fifteen figures (fourteen of which are supplemental). Embedded in those figures are 23 independent t-tests, none of which would appear to be obvious candidates for multiple comparison adjustments. However, you begin to worry. Since the chosen significance threshold for your tests was 0.05, there is nearly a 70% chance [1 – (0.95)23 = 0.693] that at least one of your conclusions is wrong34. Thinking about this more, you realize that over the course of your career you hope to publish at least 50 papers, each of which could contain an average of 20 statistical tests. This would mean that over the course of your career you are 99.9999999999999999999947% likely to publish at least one error and will undoubtedly publish many (at least those based on statistical tests). To avoid this humiliation, you decide to be proactive and impose a career-wise Bonferroni correction to your data analysis. From now on, for results with corresponding statistical tests to be considered valid, they must have a P-value of <0.00005 (0.05/1000). Going through your current manuscript, you realize that only four of the 23 tests will meet your new criteria. With great sadness in your heart, you move your manuscript into the trash folder on your desktop.
Although the above narrative may be ridiculous (indeed, it is meant to be so), the underlying issues are very real. Conclusions based on single t-tests, which are not supported by additional complementary data, may well be incorrect. Thus, where does one draw the line? One answer is that no line should be drawn, even in situations where multiple comparison adjustments would seem to be warranted. Results can be presented with corresponding P-values, and readers can be allowed to make their own judgments regarding their validity. For larger data sets, such as those from microarray studies, an estimation of either the number or proportion of likely false positives can be provided to give readers a feeling for the scope of the problem. Even without this, readers could in theory look at the number of comparisons made, the chosen significance threshold, and the number of positive hits to come up with a general idea about the proportion of false positives. Although many reviewers and readers may not be satisfied with this kind of approach, know that there are professional statisticians who support this strategy. Perhaps most importantly, understand that whatever approaches are used, data sets, particularly large ones, will undoubtedly contain errors, including both false positives and false negatives. Wherever possible, seek to confirm your own results using multiple independent methods so that you are less likely to be fooled by chance occurrence.
29This discussion assumes that the null hypothesis (of no difference) is true in all cases.
30Notice that this is the Bonferroni critical value against which all P-values would be compared.
31If the null hypothesis is true, P-values are random values, uniformly distributed between 0 and 1.
32The name is a bit unfortunate in that all of statistics is devoted to analyzing variance and ascribing it to random sources or certain modeled effects.
33These are referred to in the official ANOVA vernacular as treatment groups.
34This is true supposing that none are in fact real.
Sections 2 and 3 dealt exclusively with issues related to means. For many experiments conducted in our field, however, mean values are not the end goal. For example, we may seek to determine the frequency of a particular defect in a mutant background, which we typically report as either a proportion (e.g., 0.7) or a percentage (e.g., 70%). Moreover, we may want to calculate CIs for our sample percentages or may use a formal statistical test to determine if there is likely to be a real difference between the frequencies observed for two or more samples. In other cases, our analyses may be best served by determining ratios or fold changes, which may require specific statistical tools. Finally, it is often useful, particularly when carrying out genetic experiments, to be able to calculate the probabilities of various outcomes. This section will cover major points that are relevant to our field when dealing with these common situations.
Most readers are likely proficient at calculating the probability of two independent events occurring through application of the multiplication rule. Namely, If event A occurs 20% of the time and event B occurs 40% of the time, then the probability of event A and B both occurring is 0.2 × 0.4 = 0.08 or 8%. More practically, we may wish to estimate the frequency of EcoRI restriction endonuclease sites in the genome. Because the EcoRI binding motif is GAATTC and each nucleotide has a roughly one-in-four chance of occurring at each position, then the chance that any six-nucleotide stretch in the genome will constitute a site for EcoRI is (0.25)6 = 0.000244140625 or 1 in 4,096. Of course, if all nucleotides are not equally represented or if certain sequences are more or less prevalent within particular genomes, then this will change the true frequency of the site. In fact, GAATTC is over-represented in phage genomes but under-represented in human viral sequences (Burge et al., 1992). Thus, even when calculating straightforward probabilities, one should be careful not to make false assumptions regarding the independence of events.
In carrying out genetic studies, we will often want to determine the likelihood of obtaining a desired genotype. For example, if we are propagating an unbalanced recessive lethal mutation (let), we will need to pick phenotypically wild-type animals at each generation and then assess for the presence of the lethal mutation in the first-generation progeny. Basic Mendelian genetics (as applied to C. elegans hermaphrodites) states that the progeny of a let/+ parent will be one-fourth let/let, one-half let/+, and one-fourth +/+. Thus, among the non-lethal progeny of a let/+ parent, two-thirds will be let/+ and one-third will be +/+. A practical question is how many wild-type animals should we single-clone at each generation to ensure that we pick at least one let/+ animal? In this case, using the complement of the multiplication rule, also referred to as the probability of “at least one”, will be most germane. We start by asking what is the probability of an individual not being let/+, which in this case is one-third or 0.333? Therefore the probability of picking five animals, none of which are of genotype let/+ is (0.333)5 or 0.41%, and therefore the probability of picking at least one let/+ would be 1 − 0.041 = 99.59%. Thus, picking five wild-type animals will nearly guarantee that at least one of the F1 progeny is of our desired genotype. Furthermore, there is a (0.667)5 ≈ 13.20% chance that all five animals will be let/+.
To calculate probabilities for more-complex problems, it is often necessary to account for the total number of combinations or permutations that are possible in a given situation. In this vernacular, the three different arrangements of the letters ABC, ACB, BAC, are considered to be distinct permutations, but only one combination. Thus, for permutations the order matters, whereas for combinations it does not. Depending on the situation, either combinations or permutations may be most relevant. Because of the polarity inherent to DNA polymers, GAT and TAG are truly different sequences and thus permutations would be germane. So far as a standard mass spectroscopy is concerned, however, the peptides DAVDKEN and KENDAVD are identical, and thus combinations might be more relevant in this case.
To illustrate the process of calculating combinations and permutations, we'll first use an example involving peptides. If each of the twenty standard amino acids (aa) is used only once in the construction of a 20-aa peptide, how many distinct sequences can be assembled? We start by noting that the order of the amino acids will matter, and thus we are concerned with permutations. In addition, given the set up where each amino acid can be used only once, we are sampling without replacement. The solution can be calculated using the following generic formula: # of permutations = n!. Here n is the total number of items and “!” is the mathematical factorial symbol, such that n! = n × (n − 1) × (n − 2) … × 1. For example, 5! = 5 × 4 × 3 × 2 × 1 = 120. Also by convention, 1! and 0! are both equal to one. To solve this problem we therefore multiply 20 × 19 × 18 … 3 × 2 × 1 or 20! ≈ 2.4e18, an impressively large number. Note that because we were sampling without replacement, the incremental decrease with each multiplier was necessary to reflect the reduced choice of available amino acids at each step. Had we been sampling with replacement, where each amino acid can be used any number of times, the equation would simply be 2020 ≈ 1.1e26, an even more impressive number!
Going back to the previous genetic example, one might wish to determine the probability of picking five progeny from a parent that is let/+ where three are of genotype let/+ and two are +/+. One thought would be to use the multiplication rule where we multiply 0.667 × 0.667 × 0.667 × 0.333 × 0.333, or more compactly, (0.667)3(0.333)2 = 0.0329 or 3.29%. If this seems a bit lower than you might expect, your instincts are correct. The above calculation describes only the probability of obtaining any one particular sequence that produces three let/+ (L) and two +/+ (W) worms. For this reason, it underestimates the true frequency of interest, since there are multiple ways of getting the same combination. For example, one possible order would be WWLLL, but equally probable are WLWLL, WLLWL, WLLLW, LLLWW, LLWLW, LLWWL, LWLLW, LWWLL, and LWLWL, giving a total of ten possible permutations. Of course, unlike peptides or strands of DNA, all of the possible orders are equivalent with respect to the relevant outcome, obtaining three let/+ and two +/+ worms. Thus, we must take permutations into account in order to determine the frequency of the generic combination. Because deriving permutations by hand (as we did above) becomes cumbersome (if not impossible) very quickly, one can use the following equation where n is the total number of items with n1 that are alike and n2 that are alike, etc., up through nk.
Thus plugging in the numbers for our example, we would have 5!/3! 2! = 120/(6 × 2) = 10. Knowing the number of possible permutations we can then multiply this by the probability of getting any single arrangement of three let/+ and two +/+ worms calculated above, such that 0.0329 × 10 = 0.329 or 32.9%, a number that makes much more sense. This illustrates a more general rule regarding the probability (Pr) of obtaining specific combinations:
Pr combination = (# of permutations) × (probability of obtaining any single permutation)
Note, however, that we may often be interested in a slightly different question than the one just posed. For example, what is the probability that we will obtain at least three let/+ animals with five picks from a let/+ parent? In this case, we would have to sum the probabilities for three out of five [(5!/3! 2!) (0.0329) = .329], four out of five [(5!/4! 1!) (0.0329) = 0.165], five out of five [(0.667)5 = 0.132] let/+ animals, giving us 0.329 + 0.165 + 0.132 = 0.626 or 62.6%.
The ability to calculate permutations can also be used to determine the number of different nucleotide sequences in a 20-mer where each of the four nucleotides (G, A, T, C) is used five times. Namely, 20!/(5!)4 ≈ 1.2e10. Finally, we can calculate the number of different peptides containing five amino acids where each of the twenty amino acids is chosen once without replacement. In this case, we can use a generic formula where n is the total number of items from which we select r items without replacement.
This would give us 20!/(20 − 5)! = 20!/(15)! = 20 × 19 × 18 × 17 × 16 = 1,860,480. The same scenario carried out with replacement would simply be (20)5 = 3,200,000. Thus, using just a handful of formulas, we are empowered with the ability to make a wide range of predictions for the probabilities that we may encounter. This is important because probabilities are not always intuitive as illustrated by the classic “birthday problem”, which demonstrates that within a group of only 23 people, there is a >50% probability that at least two will share the same birthday35.
Certain types of probabilistic events can be modeled using a distribution developed by the French mathematician Siméon Denis Poisson. Specifically, the Poisson distribution can be used to predict the probability that a given number of events will occur over a stipulated interval of time, distance, space, or other related measure, when said events occur independently of one another. For example, given a known forward mutation rate caused by a chemical mutagen, what is the chance that three individuals from a collection of 1,000 F1s (derived from mutagenized P0 parents) will contain a mutation in gene X? Also, what is the chance that any F1 worm would contain two or more independent mutations within gene X?
The generic formula used to calculate such probabilities is shown below, where µ is the mean number of expected events, x is the number of times that the event occurs over a specified interval, and e is the natural log.
For this formula to predict probabilities accurately, it is required that the events be independent of each other and occur at a constant average rate over the given interval. If these criteria are violated, then the Poisson distribution will not provide a valid model. For example, imagine that we want to calculate the likelihood that a mutant worm that is prone to seizures will have two seizures (i.e., events or x) within a 5-minute interval. For this calculation, we rely on previous data showing that, on average, mutant worms have 6.2 seizures per hour. Thus, the average (μ) for a 5-minute interval would be 6.2/12 = 0.517. Plugging these numbers into the above formula we obtain P(x) = 0.080 or 8%. Note that if we were to follow 20 different worms for 5 minutes and observed six of them to have two seizures, this would suggest that the Poisson distribution is not a good model for our particular event36. Rather, the data would suggest that multiple consecutive seizures occur at a frequency that is higher than predicted by the Poisson distribution, and thus the seizure events are not independent. In contrast, had only one or two of the 20 worms exhibited two seizures within the time interval, this would be consistent with a Poisson model.
Another useful strategy for calculating probabilities, as well as other parameters of interest that are governed by chance, is sometimes referred to as the intuitive approach. This includes the practice of plugging hypothetical numbers into scenarios to maximize the clarity of the calculations and conclusions. Our example here will involve efforts to maximize the efficiency of an F2-clonal genetic screen to identify recessive maternal-effect lethal or sterile mutations (Figure 11). For this experiment, we will specify that 100 P0 adults are to be cloned singly onto plates following mutagenesis. Then ten F1 progeny from each P0 will be single-cloned, some small fraction of which will be heterozygous for a desired class of mutation (m/+). To identify mutants of interest, however, F2s of genotype m/m must be single-cloned, and their F3 progeny must be inspected for the presence of the phenotype. The question is: what is the optimal number of F2s to single-clone from each F1 plate?
Mendelian genetics states that the chance of picking an m/m F2 from an m/+ F1 parent is one in four or 25%, so picking more will of course increase the likelihood of obtaining the desired genotype. But will the returns prove diminishing and, if so, what is the most efficient practice? Table 4 plugs in real numbers to determine the frequency of obtaining m/m animals based on the number of cloned F2s. The first column shows the number of F2 animals picked per F1, which ranges from one to six. In the second column, the likelihood of picking at least one m/m animal is determined using the inverse multiplication rule. As expected, the likelihood increases with larger numbers of F2s, but diminishing returns are evident as the number of F2s increases. Columns 3–5 tabulate the number of worm plates required, the implication being that more plates are both more work and more expense. Columns six and eight calculate the expected number of m/m F2s that would be isolated given frequencies of (m/+) heterozygotes of 0.01 (10 in 1,000 F1s) or 0.001 (1 in 1,000 F1s), respectively. Here, a higher frequency would infer that the desired mutations of interest are more common. Finally, columns seven and nine show the predicted efficiencies of the screening strategies by dividing the number of isolated m/m F2s by the total number of F1 and F2 plates required (e.g., 2.50/2,000 = 1.25e–3).
Table 4. Intuitive approach to determine the maximum efficiency of an F2-clonal genetic screen.
| # of F2s/F1 | Likelihood of cloning at least one m/m | # F1 plates | # F2 plates | Total # plates | Expected # m/m isolated f = 0.01 | Efficiency (#m/m per total) f = 0.01 | Expected # m/m isolated f = 0.001 | Efficiency (#m/m per total) f= 0.001 |
|---|---|---|---|---|---|---|---|---|
| 1 | 25.0% | 1000 | 1000 | 2000 | 2.50 | 1.25e-3 | 0.250 | 1.25e-4 |
| 2 | 43.8% | 1000 | 2000 | 3000 | 4.38 | 1.46e-3 | 0.438 | 1.46e-4 |
| 3 | 57.8% | 1000 | 3000 | 4000 | 5.78 | 1.45e-3 | 0.578 | 1.45e-4 |
| 4 | 68.4% | 1000 | 4000 | 5000 | 6.84 | 1.37e-3 | 0.684 | 1.37e-4 |
| 5 | 76.3% | 1000 | 5000 | 6000 | 7.63 | 1.27e-3 | 0.763 | 1.27e-4 |
| 6 | 82.2% | 1000 | 6000 | 7000 | 8.22 | 1.17e-3 | 0.822 | 1.17e-4 |
From this we can see that either two or three F2s is the most efficient use of plates and possibly time, although other factors could potentially factor into the decision of how many F2s to pick. We can also see that the relative efficiencies are independent of the frequency of the mutation of interest. Importantly, this potentially useful insight was accomplished using basic intuition and a very rudimentary knowledge of probabilities. Of course, the outlined intuitive approach failed to address whether the optimal number of cloned F2s is 2.4 or 2.537, but as we haven't yet developed successful methods to pick or propagate fractions of C. elegans, such details are irrelevant!
We note that an online tool has been created by Shai Shaham (Shaham, 2007) that allows users to optimize the efficiency of genetic screens in C. elegans38. To use the tool, users enter several parameters that describe the specific genetic approach (e.g., F1 versus F2 clonal). The website's algorithm then provides a recommended F2-to-F1 screening ratio. Entering parameters that match the example used above, the website suggests picking two F2s for each F1, which corresponds to the number we calculated using our intuitive approach. In addition, the website provides a useful tool for calculating the screen size necessary to achieve a desired level of genetic saturation. For example, one can determine the number of cloned F1s required to ensure that all possible genetic loci will be identified at least once during the course of screening with a 95% confidence level.
In many situations, the likelihood of two events occurring is not independent. This does not mean that the two events need be totally interdependent or mutually exclusive, just that one event occurring may increase or decrease the likelihood of the other. Put another way, having prior knowledge of one outcome may change the effective probability of a second outcome. Knowing that someone has a well-worn “1997 C. elegans International Meeting” t-shirt in his drawer does not guarantee that he is an aging nerd, but it certainly does increase the probability! The area of statistics that handles such situations is known as Bayesian analysis or inference, after an early pioneer in this area, Thomas Bayes. More generally, conditional probability refers to the probability of an event occurring based on the condition that another event has occurred. Although conditional probabilities are extremely important in certain types of biomedical and epidemiological research, such as predicting disease states given a set of known factors39, this issue doesn't arise too often for most C. elegans researchers. Bayesian models and networks have, however, been used in the worm field for applications that include phylogenetic gene tree construction (Hoogewijs et al., 2008; Agarwal and States, 1996), modeling developmental processes (Sun and Hong, 2007), and predicting genetic interactions (Zhong and Sternberg, 2006). Bayesian statistics is also used quite extensively in behavioral neuroscience (Knill and Pouget, 2004; Vilares and Kording, 2011 ), which is growing area in the C. elegans field. We refer interested readers to textbooks or the web for additional information (see Appendix A).
It is common in our field to generate data that take the form of binomial proportions. Examples would include the percentage of mutant worms that arrest as embryos or that display ectopic expression of a GFP reporter. As the name implies, binomial proportions arise from data that fall into two categories such as heads or tails, on or off, and normal or abnormal. More generically, the two outcomes are often referred to as a success or failure. To properly qualify, data forming a binomial distribution must be acquired by random sampling, and each outcome must be independent of all other outcomes. Coin flips are a classic example where the result of any given flip has no influence on the outcome of any other flip. Also, when using a statistical method known as the normal approximation (discussed below), the binomial dataset should contain a minimum of ten outcomes in each category (although some texts may recommend a more relaxed minimum of five). This is generally an issue only when relatively rare events are being measured. For example, flipping a coin 50 times would certainly result in at least ten heads or ten tails, whereas a phenotype with very low penetrance might be detected only in three worms from a sample of 100. In this latter case, a larger sample size would be necessary for the approximation method to be valid. Lastly, sample sizes should not be >10% of the entire population. As we often deal with theoretical populations that are effectively infinite in size, however, this stipulation is generally irrelevant.
An aside on the role of normality in binomial proportions is also pertinent here. It might seem counterintuitive, but the distribution of sample proportions arising from data that are binary does have, with sufficient sample size, an approximately normal distribution. This concept is illustrated in Figure 12, which computationally simulates data drawn from a population with an underlying “success” rate of 0.25. As can be seen, the distribution becomes more normal with increasing sample size. How large a sample is required, you ask? The short answer is that the closer the underlying rate is to 50%, the smaller the required sample size is; with a more extreme rate (i.e., closer to 0% or 100%), a larger size is required. The requirements are reasonably met by the aforementioned minimum of ten rule.
Figure 12. Illustration of the Central Limit Theorem for binomial proportions. Panels A–D show results from a computational sampling experiment where the proportion of successes in the population is 0.25. The x axes indicate the proportions obtained from samples sizes of 10, 20, 40, and 80. The y axes indicate the number of computational samples obtained for a given proportion. As expected, larger-sized samples give distributions that are closer to normal in shape and have a narrower range of values.
To address the accuracy of proportions obtained through random sampling, we will typically want to provide an accompanying CI. For example, political polls will often report the percentage in favor of a candidate along with a 95% CI, which may encompass several percentage points to either side of the midpoint estimate40. As previously discussed in the context of means, determining CIs for sample proportions is important because in most cases we can never know the true proportion of the population under study. Although different confidence levels can be used, binomial data are often accompanied by 95% CIs. As for means, lower CIs (e.g., 90%) are associated with narrower intervals, whereas higher CIs (e.g., 99%) are associated with wider intervals. Once again, the meaning of a 95% CI is the same as that discussed earlier in the context of means. If one were to repeat the experiment 100 times and calculate 95% CIs for each repeat, on average 95 of the calculated CIs would contain the true population proportion. Thus, there is a 95% chance that the CI calculated for any given experiment contains the true population proportion.
Perhaps surprisingly, there is no perfect consensus among statisticians as to which of several methods is best for calculating CIs for binomial proportions41. Thus, different textbooks or websites may describe several different approaches. That said, for most purposes we can recommend a test that goes by several names including the adjusted Wald, the modified Wald, and the Agresti-Coull (A-C) method (Agresti and Coull, 1998; Agresti and Caffo, 2000). Reasons for recommending this test are: (1) it is widely accepted, (2) it is easy to implement (if the chosen confidence level is 95%), and (3) it gives more-accurate CIs than other straightforward methods commonly in use. Furthermore, even though this approach is based on the normal approximation method, the minimum of ten rule can be relaxed.
To implement the A-C method for a 95% CI (the most common choice), add two to both the number of successes and failures. Hence this is sometimes referred to as the plus-four or “+4” method. It then uses the doctored numbers, together with the normal approximation method, to determine the CI for the population proportion. Admittedly this sounds weird, if not outright suspicious, but empirical studies have shown that this method gives consistently better 95% CIs than would be created using the simpler method. For example, if in real life you assayed 83 animals and observed larval arrest in 22, you would change the total number of trials to 87 and the number of arrested larvae to 24. In addition, depending on the software or websites used, you may need to choose the normal approximation method and not something called the exact method for this to work as intended.
Importantly, the proportion and sample size that you report should be the actual proportion and sample size from what you observed; the doctored (i.e., plus-four) numbers are used exclusively to generate the 95% CI. Thus, in the case of the above example, you would report the proportion as 22/83 = 0.265 or 26.5%. The 95% CI would, however, be calculated using the numbers 24 and 87 to give a 95% CI of 18.2%–37.0%. Note that the +4 version of the A-C method is specific for 95% CIs and not for other intervals42. Finally, it is worth noting that CIs for proportions that are close to either 0% or 100% will get a bit funky. This is because the CI cannot include numbers <0% or >100%. Thus, CIs for proportions close to 0% or 100% will often be quite lopsided around the midpoint and may not be particularly accurate. Nevertheless, unless the obtained percentage is 0 or 100, we do not recommend doing anything about this as measures used to compensate for this phenomenon have their own inherent set of issues. In other words, if the percentage ranges from 1% to 99%, use the A-C method for calculation of the CI. In cases where the percentage is 0% or 100%, instead use the exact method.
Very often we will want to compare two proportions for differences. For example, we may observe 85% larval arrest in mutants grown on control RNAi plates and 67% arrest in mutants on RNAi-feeding plates targeting gene X. Is this difference significant from a statistical standpoint? To answer this, two distinct tests are commonly used. These are generically known as the normal approximation and exact methods. In fact, many website calculators or software programs will provide the P-value calculated by each method as a matter of course, although in some cases you may need to select one method. The approximation method (based on the so-called normal distribution) has been in general use much longer, and the theory behind this method is often outlined in some detail in statistical texts. The major reason for the historical popularity of the approximation method is that prior to the advent of powerful desktop computers, calculations using the exact method simply weren't feasible. Its continued use is partly due to convention, but also because the approximation and exact methods typically give very similar results. Unlike the normal approximation method, however, the exact method is valid in all situations, such as when the number of successes is less than five or ten, and can thus be recommended over the approximation method.
Regardless of the method used, the P-value derived from a test for differences between proportions will answer the following question: What is the probability that the two experimental samples were derived from the same population? Put another way, the null hypothesis would state that both samples are derived from a single population and that any differences between the sample proportions are due to chance sampling. Much like statistical tests for differences between means, proportions tests can be one- or two-tailed, depending on the nature of the question. For the purpose of most experiments in basic research, however, two-tailed tests are more conservative and tend to be the norm. In addition, analogous to tests with means, one can compare an experimentally derived proportion against a historically accepted standard, although this is rarely done in our field and comes with the possible caveats discussed in Section 2.3. Finally, some software programs will report a 95% CI for the difference between two proportions. In cases where no statistically significant difference is present, the 95% CI for the difference will always include zero.
A question that may arise when comparing more than two binomial proportions is whether or not multiple comparisons should be factored into the statistical analysis. The issues here are very similar to those discussed in the context of comparing multiple means (Section 3). In the case of proportions, rather than carrying out an ANOVA, a Chi-square test (discussed below) could be used to determine if any of the proportions are significantly different from each other. Like an ANOVA, however, this may be a somewhat less-than-satisfying test in that a positive finding would not indicate which particular proportions are significantly different. In addition, FDR and Bonferroni-type corrections could also be applied at the level of P-value cutoffs, although these may prove to be too conservative and could reduce the ability to detect real differences (i.e., the power of the experiment).
In general, we can recommend that for findings confirmed by several independent repeats, corrections for multiple comparisons may not be necessary. We illustrate our rationale with the following example. Suppose you were to carry out a genome-wide RNAi screen to identify suppressors of larval arrest in the mutant Y background. A preliminary screen might identify ∼1,000 such clones ranging from very strong to very marginal suppressors. With retesting of these 1,000 clones, most of the false positives from the first round will fail to suppress in the second round and will be thrown out. A third round of retesting will then likely eliminate all but a few false positives, leaving mostly valid ones on the list. This effect can be quantified by imagining that we carry out an exact binomial test on each of ∼20,000 clones in the RNAi library, together with an appropriate negative control, and chose an α level (i.e., the statistical cutoff) of 0.05. By chance alone, 5% or 1,000 out of 20,000 would fall below the P-value threshold. In addition, let's imagine that 100 real positives would also be identified giving us 1,100 positives in total. Admittedly, at this point, the large majority of identified clones would be characterized as false positives. In the second round of tests, however, the large majority of true positives would again be expected to exhibit statistically significant suppression, whereas only 50 of the 1,000 false positives will do so. Following the third round of testing, all but two or three of the false positives will have been eliminated. These, together with the ∼100 true positives, most of which will have passed all three tests, will leave a list of genes that is strongly enriched for true positives. Thus, by carrying out several experimental repeats, additional correction methods are not needed.
At times one may be interested in calculating the probability of obtaining a particular proportion or one that is more extreme, given an expected frequency. For example, what are the chances of tossing a coin 100 times and getting heads 55 times? This can be calculated using a small variation on the formulae already presented above.
Here n is the number of trials, Y is the number of positive outcomes or successes, and p is the probability of a success occurring in each trial. Thus we can determine that the chance of getting exactly 55 heads is quite small, only 4.85%. Nevertheless, given an expected proportion of 0.5, we intuitively understand that 55 out of 100 heads is not an unusual result. In fact, we are probably most interested in knowing the probability of getting a result at least as or more extreme than 55 (whether that be 55 heads or 55 tails). Thus our probability calculations must also include the results where we get 56, 57, 58…100 heads as well as 45, 44, 43 …0 heads. Adding up these probabilities then tells us that we have a 36.8% chance of obtaining at least 55 heads or tails in 100 tosses, which is certainly not unusual. Rather than having to calculate each probability and adding them up, however, a number of websites will do this for you. Nevertheless, be alert and understand the principles behind what you are doing, as some websites may only give you the probability of ≥55%, whereas what you really may need is the summed probability of both ≥55% and ≤45%.
One of the assumptions for using the binomial distribution is that our population size must be very large relative to our sample size43. Thus, the act of sampling itself should not appreciably alter the course of future outcomes (i.e., the probability is fixed and does not change each trial). For example, if we had a (very large) jar with a million marbles, half of them black and half of them white, removing one black marble would not grossly alter the probability of the next marble being black or white. We can therefore treat these types of situations as though the populations were infinite or as though we were sampling with replacement. In contrast, with only ten marbles (five white and five black), picking a black marble first would reduce the probability of the next marble being black from 50% (5/10) to 44.4% (4/9), while increasing the probability of the next marble being white to 55.6% (5/9)44. For situations like this, in which the act of sampling noticeably affects the remaining population, the binomial is shelved in favor of something called the hyper-geometric distribution. For example, in the case of the ten marbles, the probability of picking out five marbles, all of which are black, is 0.0040 using the hypergeometric distribution. In contrast, the binomial applied to this situation gives an erroneously high value of 0.031.
For our field, we often see hyper-geometric calculations applied to computational or genomics types of analyses. For example, imagine that we have carried out an RNA-seq experiment and have identified 1,000 genes that are mis-expressed in a particular mutant background. A gene ontology (GO) search reveals that 13 of these genes encode proteins with a RING domain. Given that there are 152 annotated RING domain–containing proteins in C. elegans, what is the probability that at least 13 would arise by chance in a dataset of this size? The rationale for applying a hyper-geometric distribution to this problem would be as follows. If one were to randomly pick one of ∼20,000 worm proteins out of a hat, the probability of it containing a RING domain would be 152/20,000 (0.00760). This leaves 151 remaining RING proteins that could be picked in future turns. The chance that the next protein would contain a RING domain is then 151/19,999 (0.00755). By the time we have come to the thirteenth RING protein in our sample of 1,000 differentially expressed genes, our chances might be something like 140/19,001 (0.00737). Plugging the required numbers into both binomial and hyper-geometric calculators45 (available on the web), we get probabilities of 0.0458 and 0.0415, respectively. Admittedly, in this case the hyper-geometric method gives us only a slightly smaller probability than the binomial. Here the difference isn't dramatic because the population size (20,000) is not particularly small.
We would also underscore the importance of being conservative in our interpretations of GO enrichment studies. In the above example with RING finger proteins, had the representation in our dataset of 1,000 genes been 12 instead of 13, the probability would have been greater than 0.05 (0.0791 and 0.0844 by hyper-geometric and binomial methods, respectively). Furthermore, we need to consider that there are currently several thousand distinct GO terms that are currently used to classify C. elegans genes. Thus, the random chance of observing over-representation within any one particular GO class will be much less than observing over-representation within some—but no particular—GO class. Going back to marbles, if we had an urn with 100 marbles of ten different colors (10 marbles each), the chance that a random handful of 5 marbles would contain at least 3 of one particular color is only 0.00664. However, the chance of getting at least three out of five the same color is 0.0664. Thus, for GO over-representation to be meaningful, we should look for very low P-values (e.g., ≤1e–5).
Multinomial proportions or distributions refer to data sets where outcomes are divided into three or more discrete categories. A common textbook example involves the analysis of genetic crosses where either genotypic or phenotypic results are compared to what would be expected based on Mendel's laws. The standard prescribed statistical procedure in these situations is the Chi-square goodness-of-fit test, an approximation method that is analogous to the normal approximation test for binomials. The basic requirements for multinomial tests are similar to those described for binomial tests. Namely, the data must be acquired through random sampling and the outcome of any given trial must be independent of the outcome of other trials. In addition, a minimum of five outcomes is required for each category for the Chi-square goodness-of-fit test to be valid. To run the Chi-square goodness-of-fit test, one can use standard software programs or websites. These will require that you enter the number of expected or control outcomes for each category along with the number of experimental outcomes in each category. This procedure tests the null hypothesis that the experimental data were derived from the same population as the control or theoretical population and that any differences in the proportion of data within individual categories are due to chance sampling.
As is the case with binomials, exact tests can also be carried out for multinomial proportions. Such tests tend to be more accurate than approximation methods, particularly if the requirement of at least five outcomes in each category cannot be met. Because of the more-complicated calculations involved, however, exact multinomial tests are less commonly used than the exact binomial test, and web versions are currently difficult to come by. The good news is that, like the binomial tests, the approximate and exact methods for multinomials will largely yield identical results. Also make sure that you don't confuse the Chi-square goodness-of-fit test with the Chi-square test of independence, which also has an exact version termed the Fisher's exact test.
Although many of us will probably not require the Chi-square goodness-of-fit test to sort out if our proportion of yellow wrinkled peas is what we might have expected, understand that this test can be used for any kind of sample data where more than two categories are represented. Imagine that we are studying a gene in which mutations lead to pleiotropy, meaning that a spectrum of distinct phenotypes is observed. Here, the proportion of animals displaying each phenotype could be compared across different alleles of the same gene to determine if specific mutations affect certain developmental processes more than others. In other instances, numerical data, such as the number of mRNA molecules in an embryo, may also benefit from imposing some broader categorization. For example, embryos might be divided into those containing 0–10, 11–50, 51–200, and >200 transcripts. These outcomes could then be compared across different mutant backgrounds or at different developmental time points to identify broad categorical differences in expression. In all of the above cases, a Chi-square goodness-of-fit test would be appropriate to determine if any differences in the observed proportions are statistically significant.
35Proofs showing this abound on the internet.
36Although this may seem intuitive, we can calculate this using some of the formulae discussed above. Namely, this boils down to a combinations problem described by the formula: Pr(combination) = (# permutations) (probability of any single permutation). For six events in 20, the number of permutations = 20!/6! 14! = 38,760. The probability of any single permutation = (0.08)6 (0.92)14 = 8.16e-8. Multiplying these together we obtain a value of 0.00316. Thus, there is about a 0.3% chance of observing six events if the events are indeed random and independent of each other. Of course, what we really want to know is the chance of observing at least six events, so we also need to include (by simple addition) the probabilities of observing 7, 8, …20 events. For seven events, the probability is only 0.000549, and this number continues to decrease precipitously with increasing numbers of events. Thus, the chance of observing at least six events is still <0.4%, and thus we would suspect that the Poisson distribution does not accurately model our event.
39Calculating the probability that a medical patient has a particular (often rare) disease given a positive diagnostic test result is a classic example used to illustrate the utility of Baye's Theorem. Two complimentary examples on the web can be found at: http://vassarstats.net/bayes.html and http://www.tc3.edu/instruct/sbrown/stat/falsepos.htm.
40This will often be stated in terms of a margin of error rather than the scientific formalism of a confidence interval.
41The reasons for this are complex and due in large part to the demonstrated odd behavior of proportions (See Agresti and Coull 1998, Agresti and Caffo 2000; and Brown et al., 2001).
42A more precise description of the A-C method is to add the square of the appropriate z-value to the denominator and half of the square of the z-value to the numerator. Conveniently, for the 95% CI, the z-value is 1.96 and thus we add 1.962 = 3.84 (rounded to 4) to the denominator and 3.84/2 = 1.92 (rounded to 2) to the numerator. For a 99% A-C CI, we would add 6.6 (2.5752) to the denominator and 3.3 (6.6/2) to the numerator. Note that many programs will not accept anything other than integers (whole numbers) for the number of successes and failures and so rounding is necessary.
43Other assumptions for the binomial include random sampling, independence of trials, and a total of two possible outcomes.
44Card counters in Las Vegas use this premise to predict the probability of future outcomes to inform their betting strategies, which makes them unpopular with casino owners.
45Note that the numbers you will need to enter for each method are slightly different. The binomial calculators will require you to enter the probability of a success (0.00760), the number of trials (1,000), and the number of successes (13). The hyper-geometric calculator will require you to enter the population size (20,000), the number of successes in the population (152), the sample size (1,000), and the number of success in the sample (13). Also note that because of the computational intensity of the hyper-geometric approach, many websites will not accommodate a population size of >1,000. One website that will handle larger populations (http://keisan.casio.com/has10/SpecExec.cgi?id=system/2006/1180573202) may use an approximation method.
It is common in biology for relative changes to be more germane than incremental ones. There are two principal reasons for this. One is that certain biological phenomena can only be properly described and understood through relative changes. For example, if we were to count the number of bacterial cells in a specified volume of liquid culture every hour, we might derive the following numbers: 1,000, 2,000, 4,000, 8,000, 16,000. The pattern is clear; the cells are doubling every hour. Conversely, it would be ridiculous to take the mean of the observed changes in cell number and to state that, on average, the cells increase by 3,750 each hour with a 95% CI of −1,174.35 to 8,674.35! The second reason is due to experimental design. There are many instances where variability between experiments or specimens makes it difficult, if not impossible, to pool mean values from independent repeats in a productive way. Rather, the ratio of experimental and control values within individual experiments or specimens should be our focus. One example of this involves quantifying bands on a western blot and is addressed below. Most traditional statistical approaches, however, are oriented toward the analysis of incremental changes (i.e., where change is measured by subtraction). Thus, it may not always be clear how to analyze data when the important effects are relative.
As an example of a situation in which ratios are likely to be most useful, we consider the analysis of a western blot (Figure 13) (also see Gassmann et al., 2009). This schematic blot shows the outcome of an experiment designed to test the hypothesis that loss of gene y activity leads to changes in the expression of protein X in C. elegans. In one scenario, the three blots (A–C) could represent independent biological repeats with lanes 1–3 serving as technical (e.g., loading) repeats. In another scenario, the three blots could serve as technical repeats with lanes 1–3 representing independent biological repeats. Regardless, either scenario will give essentially the same result. Quantification of each band, based on pixel intensity, is indicated in blue46. Based on Figure 13, it seems clear that loss of gene y leads to an increase in the amount of protein X. So does the statistical analysis agree?
Figure 14 shows the results of carrying out the statistical analysis in several different ways. This includes, for illustrative purposes, seven distinct two-tailed t-tests (1–7). In t-tests 1–3, data from wild-type and mut y bands were pooled within individual blots to obtain an average. Interestingly, only one of the three, blot A, showed a statistically significant difference (P ≤ 0.05) between wild type and mut y, despite all three blots appearing to give the same general result. In this case, the failure of blots B and C to show a significant difference is due to slightly more variability between samples of the same kind (i.e., wild type or mut y) and because with an n = 3, the power of the t-test to detect small or even moderate differences is weak. The situation is even worse when we combine subsets of bands from different blots, such as pooled lanes 1, 2, and 3 (t-tests 4–6). Pooling all of the wild-type and mut y data (t-test 7) does, however, lead to a significant difference (P = 0.0065).
Figure 14. Statistical analysis of western blot data from Figure 13. A summary of test options is shown.
So was the t-test the right way to go? Admittedly, it probably wasn't very satisfying that only one of the first three t-tests indicated a significant difference, despite the raw data looking similar for all three. In addition, we need to consider whether or not pooling data from different blots was even kosher. On the one hand, the intensity of the protein X band in any given lane is influenced by the concentration of protein X in the lysate, which is something that we care about. On the other hand, the observed band intensity is also a byproduct of the volume of lysate loaded, the efficiency of protein transfer to the membrane, the activity of the radiolabel or enzymes used to facilitate visualization, and the length of the exposure time, none of which are relevant to our central question! In fact, in the case of western blots, comparing intensities across different blots is really an apples and oranges proposition, and thus pooling such data violates basic principles of logic47. Thus, even though pooling all the data (t-test 7) gave us a sufficiently low P-value as to satisfy us that there is a statistically significant difference in the numbers we entered, the premise for combining such data was flawed scientifically.
The last test shown in Figure 14 is the output from confidence interval calculations for two ratios. This test was carried out using an Excel tool that is included in this chapter48. To use this tool, we must enter for each paired experiment the mean (termed “estimate”) and the SE (“SE of est”) and must also choose a confidence level (Figure 15). Looking at the results of the statistical analysis of ratios (Figure 14), we generally observe much crisper results than were provided by the t-tests. For example, in the three cases where comparisons were made only within individual blots, all three showed significant differences corresponding to P < 0.05 and two (blots A and B) were significant to P < 0.0149. In contrast, as would be expected, combining lane data between different blots to obtain ratios did not yield significant results, even though the ratios were of a similar magnitude to the blot-specific data. Furthermore, although combining all values to obtain means for the ratios did give P < 0.05, it was not significant at the α level of 0.01. In any case, we can conclude that this statistical method for acquiring confidence intervals for ratios is a clean and powerful way to handle this kind of analysis.
It is also worth pointing out that there is another way in which the t-test could be used for this analysis. Namely, we could take the ratios from the first three blots (3.33, 3.41, and 2.48), which average to 3.07, and carry out a one-sample two-tailed t-test. Because the null hypothesis is that there is no difference in the expression of protein X between wild-type and mut y backgrounds, we would use an expected ratio of 1 for the test. Thus, the P-value will tell us the probability of obtaining a ratio of 3.07 if the expected ratio is really one. Using the above data points, we do in fact obtain P = 0.02, which would pass our significance cutoff. In fact, this is a perfectly reasonable use of the t-test, even though the test is now being carried out on ratios rather than the unprocessed data. Note, however, that changing the numbers only slightly to 3.33, 4.51, and 2.48, we would get a mean of 3.44 but with a corresponding P-value of 0.054. This again points out the problem with t-tests when one has very small sample sizes and moderate variation within samples.
There is also an important point to be made with respect to ratios that concerns the mean value that you would report. Based on the above paragraph, the mean of the three ratios is 3.07. However, looking at t-test 7, which used the pooled data, we can see that the ratio calculated from the total means would be 477/167 = 2.86. This points out a rather confounding property of ratio arithmetic. Namely, that the mean of the ratios (MoR; in this case 3.07) is usually not equal to the ratio of the means (RoM; 2.86). Which of the two you choose to use to report will depend on the question you are trying to answer.
To use a non-scientific (but intuitive) example, we can consider changes in housing prices over time. In a given town, the current appraised value of each house is compared to its value 20 years prior. Some houses may have doubled in value, whereas others may have quadrupled (Table 5). Taking an average of the ratios for individual houses (i.e., the relative increase)—the MoR approach—allows us to determine that the mean increase in value has been 3-fold. However, it turns out that cheaper houses (those initially costing ≤$100,000) have actually gone up about 4-fold on average, whereas more-expensive homes (those initially valued at ≥$300,000) have generally only doubled. Thus, the total increase in the combined value of all the homes in the neighborhood has not tripled but is perhaps 2.5-fold higher than it was 20 years ago (the RoM approach).
Table 5. A tinker-toy illustration for increases in house prices in TinyTown (which has only two households).
| Before | After | Relative Increase | |
|---|---|---|---|
| $100,000 | $400,000 | 4 | |
| $300,000 | $600,000 | 2 | |
| Means | $200,000 | $500,000 | MoR↓ |
| RoM→ | 2.5 | 3 |
Which statistic is more relevant? Well, if you're the mayor and if property taxes are based on the appraised value of homes, your total intake will be only 2.5 times greater than it was 20 years ago. If, on the other hand, you are writing a newspaper article and want to convey the extent to which average housing prices have increased over the past 20 years, 3-fold would seem to be a more salient statistic. In other words, MoR tells us about the average effect on individuals, whereas RoM conveys the overall effect on the population as a whole. In the case of the western blot data, 3.07 (i.e., the MoR) is clearly the better indicator, especially given the stated issues with combining data from different blots. Importantly, it is critical to be aware of the difference between RoM and MoR calculations and to report the statistic that is most relevant to your question of interest.
Data from studies where relative or exponential changes are pervasive may also benefit from transformation to log scales. For example, transforming to a log scale is the standard way to obtain a straight line from a slope that changes exponentially. This can make for a more straightforward presentation and can also simplify the statistical analysis (see Section 6.4 on outliers). Thus, transforming 1, 10, 100, 1,000 into log10 gives us 0, 1, 2, 3. Which log base you choose doesn't particularly matter, although ten and two are quite intuitive, and therefore popular. The natural50 log (∼2.718), however, has historical precedent within certain fields and may be considered standard. In some cases, back transformation (from log scale to linear) can be done after the statistical analysis to make the findings clearer to readers.
For some areas of research (such as ecology, field biology, and psychology), modeling, along with its associated statistics, is a predominant form of analysis. This is not the case for most research conducted in the worm field or, for that matter, by most developmental geneticists or molecular biologists. Correlation, in contrast, can be an important and useful concept. For this reason, we include a substantive, although brief, section on correlation, and a practically non-existent section on modeling.
Correlation describes the co-variation of two variables. For example, imagine that we have a worm strain that expresses reporters for two different genes, one labeled with GFP, the other with mCherry51. To see if expression of the two genes is correlated, GFP and mCherry are measured in 50 individual worms, and the data are plotted onto a graph known as a scatterplot. Here, each worm is represented by a single dot with associated GFP and mCherry values corresponding to the x and y axes, respectively (Figure 16). In the case of a positive correlation, the cloud of dots will trend up to the right. If there is a negative correlation, the dots will trend down to the right. If there is little or no correlation, the dots will generally show no obvious pattern. Moreover, the closer the dots come to forming a unified tight line, the stronger the correlation between the variables. Based on Figure 16, it would appear that there is a positive correlation, even if the dots don't fall exactly on a single line. Importantly, it matters not which of the two values (GFP or mCherry) is plotted on the x or the y axes. The results, including the statistical analysis described below, will come out exactly the same.
Figure 16. Scatterplot of GFP expression versus mCherry. The correlation coefficient is ∼0.68. The units on the axes are arbitrary.
The extent of correlation between two variables can be quantified through calculation of a statistical parameter termed the correlation coefficient (a.k.a. Pearson's product moment correlation coefficient, Pearson's r, or just r). The formula is a bit messy and the details are not essential for interpretation. The value of r can range from −1 (a perfect negative correlation) to 1 (a perfect positive correlation), or can be 052 in the case of no correlation. Thus, depending on the tightness of the correlation, values will range from close to zero (weak or no correlation) to 1 or −1 (perfect correlation). In our example, if one of the two genes encodes a transcriptional activator of the other gene, we would expect to see a positive correlation. In contrast, if one of the two genes encodes a repressor, we should observe a negative correlation. If expression of the two genes is in no way connected, r should be close to zero, although random chance would likely result in r having either a small positive or negative value. Even in cases where a strong correlation is observed, however, it is important not to make the common mistake of equating correlation with causation53.
Like other statistical parameters, the SD, SE, and 95% CI can be calculated for r. In addition, a P-value associated with a given r can be determined, which answers the following question: What is the probability that random chance resulted in a correlation coefficient as far from zero as the one observed? Like other statistical tests, larger sample sizes will better detect small correlations that are statistically significant. Nevertheless, it is important to look beyond the P-value in assessing biological significance, especially if r is quite small. The validity of these calculations also requires many of the same assumptions described for other parametric tests including the one that the data have something close to a normal distribution. Furthermore, it is essential that the two parameters are measured separately and that the value for a given x is not somehow calculated using the value of y and vice versa.
Examples of six different scatterplots with corresponding r and P-values are shown in Figure 17. In addition to these values, a black line cutting through the swarm of red dots was inserted to indicate the slope. This line was determined using a calculation known as the least squares or linear least squares method. The basic idea of this method is to find a straight line that best represents the trend indicated by the data, such that a roughly equal proportion of data points is observed above and below the line. Finally, blue dashed lines indicate the 95% CI of the slope. This means that we can be 95% certain that the true slope (for the population) resides somewhere between these boundaries.
Panels A–C of Figure 17 show examples of a strong (r = 0.86), weak (r = −0.27), and nonexistent (r = 0.005) correlation, respectively. The purple line in panel B demonstrates that a slope of zero can be fit within the 95% CI, which is consistent with the observed P-value of 0.092. Panel D illustrates that although small-sized samples can give the impression of a strong correlation, the P-value may be underwhelming because chance sampling could have resulted in a similar outcome. In other words, similar to SD, r is not affected by sample size54, but the P-value most certainly will be. Conversely, a large sample size will detect significance even when the correlation coefficient is relatively weak. Nevertheless, for some types of studies, a small correlation coefficient with a low P-value might be considered scientifically important. Panels E and F point out the dangers of relying just on P-values without looking directly at the scatterplot. In Panel E, we have both a reasonably high value for r along with a low P-value. Looking at the plot, however, it is clear that a straight line is not a good fit for these data points, which curve up to the right and eventually level out. Thus, the reported r and P-values, though technically correct, would misrepresent the true nature of the relationship between these variables. In the case of Panel F, r is effectively zero, but it is clear that the two variables have a very strong relationship. Such examples would require additional analysis, such as modeling, which is described briefly below.
Another very useful thing about r is that it can be squared to give R2 (or r2), also called the coefficient of determination. The reason R2 is useful is that it allows for a very easy interpretation of the relationship between the two variables. This is best shown by example. In the case of our GFP/mCherry experiment, we obtained r = 0.68, and squaring this gives us 0.462. Thus, we can say that 46.2% of the variability in mCherry can be explained by differences in the levels of GFP. The rest, 53.8%, is due to other factors. Of course, we can also say that 46.2% of the variability in GFP can be explained by differences in the levels of mCherry, as the R2 itself does not imply a direction. Of course if GFP is a reporter for a transcription factor and mCherry is a reporter for a structural gene, a causal relationship, along with a specific regulatory direction, is certainly suggested. In this case, additional experiments would have to be carried out to clarify the underlying biology.
The basic idea behind modeling and regression methods is to come up with an equation that can make useful predictions or describe the behavior of a system. In simple linear regression, a single predictor or independent variable, such as the GFP intensity of a heat-shock reporter, might be used to predict the behavior of a response or dependent variable, such as the life span of a worm55. The end result would be an equation56 that describes a line that is often, although not always, straight57. Multiple regression is an extension of simple linear regression, but it utilizes two or more variables in the prediction58. A classic example of multiple regression used in many statistics texts and classes concerns the weight of bears. Because it's not practical to weigh bears in the field, proxy measures such as head circumference, body length, and abdominal girth are acquired and fitted to an equation (by a human-aided computer or a computer-aided human), such that approximate weights can be inferred without the use of a scale. Like single and multiple linear regression, nonlinear regression also fits data (i.e., predictive variables) to a curve that can be described by an equation. In some cases, the curves generated by nonlinear regression may be quite complex. Unlike linear regression, nonlinear regression cannot be described using simple algebra. Nonlinear regression is an iterative method, and the mathematics behinds its workings are relatively complex. It is used in a number of fields including pharmacology. Logistic regression uses one or more factors to predict the probability or odds of a binary or dichotomous outcome, such as life or death. It is often used to predict or model mortality given a set of factors; it is also used by employers in decisions related to hiring or by government agencies to predict the likelihood of criminal recidivism59.
46Admittedly, standard western blots would also contain an additional probe to control for loading variability, but this has been omitted for simplification purposes and would not change the analysis following adjustments for differences in loading.
47A similar, although perhaps slightly less stringent argument, can be made against averaging cycle numbers from independent qRT-PCR runs. Admittedly, if cDNA template loading is well controlled, qRT-PCR cycle numbers are not as prone to the same arbitrary and dramatic swings as bands on a western. However, subtle differences in the quality or amount of the template, chemical reagents, enzymes, and cycler runs can conspire to produce substantial differences between experiments.
48This Excel tool was developed by KG.
49The maximum possible P-values can be inferred from the CIs. For example, if a 99% CI does not encompass the number one, the ratio expected if no difference existed, then you can be sure the P-value from a two-tailed test is <0.01.
50Admittedly, there is nothing particularly “natural” sounding about 2.718281828…
51An example of this is described in Doitsidou et al., 2007
52In the case of no correlation, the least-squares fit (which you will read about in a moment) will be a straight line with a slope of zero (i.e., a horizontal line). Generally speaking, even when there is no real correlation, however, the slope will always be a non-zero number because of chance sampling effects.
53For example, nations that that supplement their water with fluoride have higher cancer rates. The reason is not because fluoride is mutagenic. It is because fluoride supplements are carried out by wealthier countries where health care is better and people live longer. Since cancer is largely a disease of old age, increased cancer rates in this case simply reflect a wealthier long-lived population. There is no meaningful cause and effect. On a separate note, it would not be terribly surprising to learn that people who write chapters on statistics have an increased tendency to become psychologically unhinged (a positive correlation). One possibility is that the very endeavor of a writing about statistics results in authors becoming mentally imbalanced. Alternatively, volunteering to write a statistics chapter might be a symptom of some underlying psychosis. In these scenarios cause and effect could be occurring, but we don't know which is the cause and which is the effect.
54In truth, SD is affected very slightly by sample size, hence SD is considered to be a “biased” estimator of variation. The effect, however, is small and generally ignored by most introductory texts. The same is true for the correlation coefficient, r.
55Rea et al. (2005) Nat. Genet. 37, 894-898. In this case, the investigators did not conclude causation but nevertheless suggested that the reporter levels may reflect a physiological state that leads to greater longevity and robust health. Furthermore, based on the worm-sorting methods used, linear regression was not an applicable outcome of their analysis.
56The standard form of simple linear regression equations takes the form y = b1x + b0, where y is the predicted value for the response variable, x is the predictor variable, b1 is the slope coefficient, and b0 is the y-axis intercept. Thus, because b1 and b0 are known constants, by plugging in a value for x, y can be predicted. For simple linear regression where the slope is a straight line, the slope coefficient will be the same as that derived using the least-squares method.
57Although seemingly nonsensical, the output of a linear regression equation can be a curved line. The confusion is the result of a difference between the common non-technical and mathematical uses of the term “linear”. To generate a curve, one can introduce an exponent, such as a square, to the predictor variable (e.g., x2). Thus, the equation could look like this: y = b1x2 + b0.
58A multiple regression equation might look something like this: Y = b1X1 + b2X2 - b3X3 + b0, where X1-3 represent different predictor variables and b1-3 represent different slope coefficients determined by the regression analysis, and b0 is the Y-axis intercept. Plugging in the values for X1-3, Y could thus be predicted.
59Even without the use of logistic regression, I can predict with near 100% certainty that I will never agree to author another chapter on statistics! (DF)
Several issues can arise with small sample sizes. One is that with weak statistical power, we may simply fail to detect a finding of interest, a point that is addressed below. Even when we do detect a significant effect, however, our conclusions may be undermined because one of the underlying assumptions of many statistical tests—that the population from which the data are derived is approximately normally distributed—is not true. This is a bit of a chicken and egg conundrum. If our sample size is sufficiently large (e.g., >30), then we can check to see if the underlying population is likely to have a normal (or “normal enough”) distribution. If it does, then we're set. If not, we may still be safe because our sample size is sufficient to compensate for lack of normality in the population. Put another way, most statistical tests are robust to all but the most skewed distributions provided that the sample size is large enough. Conversely, with a small sample size, we can't tell much, or perhaps anything, about the underlying normality of the population. Moreover, if the population deviates far enough from normal, then our statistical tests will not be valid.
So, what to do? As already discussed in earlier sections, in some cases it may be reasonable to assume that the underlying distribution is likely normal enough to proceed with the test. Such a decision could be reasonable if this coincides with accepted standards in the field or in cases where the laboratory has previously generated similar larger data sets and shown them to have approximately normal distributions. In other cases, you may decide that collecting additional data points is necessary and justified. Alternatively, you may need to consider using a non-parametric statistical approach for which normality of the data is not a prerequisite (discussed below). Typically, non-parametric tests will have less power, however, so the effects may need to be stronger to achieve statistical significance. If you are uncertain about what to do, consulting a nearby statistician is recommended. In general, one should be cautious about interpreting P-values, especially ones that would be considered borderline (e.g., P = 0.049), when normality is uncertain and sample sizes are small.
We can also say that a sample size is too small when real effects that would be considered biologically interesting or important fail to be detected or supported by our analyses. Such cases may be referred to as false negatives or Type II errors. Of course, we are seldom in a position of knowing a priori what any outcome should be. Otherwise, why would we be doing the experiment? Thus, knowing when a Type II error has occurred is not possible. Likewise, knowing when a false positive or Type I error has occurred is also impossible. In this latter case, however, the chosen α level represents a stated degree of acceptable risk that a false positive will sneak through. So what should be the allowable risk for a false negative? There is no simple answer to this. In cases where significant health or environmental consequences could arise, the acceptable level of risk may be very low. In contrast, if we are screening an entire genome where we are likely to uncover hundreds or thousands of positive hits, missing a few genes may not be a problem.
The branch of statistics that deals with issues related to false-negative findings is called power analysis. Power analysis answers the following question: If there is a real effect of a certain magnitude, what is the probability that a study of a given size will detect it? Put another way, if the experiment was repeated many times, what fraction would lead to statistically significant outcomes? The answer to this will depend on several factors. Detecting a statistically significant effect is easier when the magnitude of the effect (e.g., the difference between means) is larger and when the variation within samples (e.g., SD) is smaller. In addition, false negatives are obviously more likely to occur with lower α levels than with higher ones (e.g., 0.001 versus 0.05).
In the case of clinical drug trials, the relevance of statistical power is self-evident. Pharmaceutical companies want to be efficient with their time and money, but not at the expense of falsely concluding that a drug is without significant benefits60. Thus, prior to any clinical trial, a power analysis is carried out to determine how many subjects must undergo the treatment in order for the study to stand a good chance of detecting a benefit of some specified size. Presumably, failing to detect an effect that is smaller in magnitude than the agreed-upon cutoff would be okay because a relatively ineffective drug would have little commercial value. Power analysis is also critical to biological field research, where collecting samples may be time consuming and costly. In other words, why spend a year chasing after data if an initial power test tells you that you'll be unlikely to detect an effect that you'd consider essential for the endeavor to be worthwhile?
Admittedly, power analysis is not something that springs to the minds of most C. elegans researchers prior to conducting an experiment. We tend to run the experiment with what we think is a reasonable number of specimens and just see what happens. There are potentially two problems with this “shoot from the hip” approach. One is that we may fail to detect true positives of interest. The second is that what we may be doing is already overkill. Namely, our sample sizes may be larger than necessary for detecting biologically significant effects. In particular, if we are doing genome-wide screens, it is in our interest to be as efficient with our time (and money) as possible.
Rather than discussing the formulas that go into calculating power, this section contains links to Excel tools, along with an instructional manual, that can be used to calculate the power of an analysis when comparing means, proportions, and other statistical parameters of interest. In addition, a number of websites and software programs can also serve this purpose. Our intention is that these tools be used by investigators to make accurate projections as to the sample size that will be required to observe effects of a given magnitude. For our example, we will imagine that we are testing RNAi feeding clones that correspond to several hundred transcription factors to see if they affect expression of an embryonic GFP reporter at the comma stage. Because quantifying expression in individual embryos is fairly time consuming, we want to calculate the minimum number of embryos required per RNAi strain, such that we have at least a 90% chance of identifying RNAi clones that lead to some minimum acceptable fold-change. Based on what we know about the biology of the system, we decide that expression increases or decreases of at least 1.5-fold are likely to be most relevant, although slightly smaller changes could also be of interest.
First we analyze GFP expression in 100 embryos from control RNAi plates. We find that the average number of pixels per embryo is 5000, that the SD = 2000, and thus the coefficient of variation is therefore 0.4 (2000/5000). We also learn that expression in comma-stage embryos is approximately normally distributed. For an effect to be of interest then, the average embryonic expression would have to be >7500 or <3300. In addition, we will assume that the SDs of the test samples vary proportionally with the mean. In other words, the SD for our test clones will be identical to our control in cases where there is no difference in mean expression but will be proportionally larger or smaller when RNAi enhances or decreases expression, respectively. This latter assumption is common and fairly intuitive given that larger means are typically associated with larger SDs, including situations where the coefficient of variation remains constant. Finally, we choose the standard α of 0.05.
Plugging these numbers into the Excel tool, we find that with a power of 90%, 18 embryos should be sufficient to detect a 1.5-fold (or 50%) increase in mean GFP expression, whereas 9 embryos are sufficient to detect a 1.5-fold (or 34%) decrease (using a two-tailed t-test; Figure 18A, B). Playing with the tool, we also notice that increasing our sample size to 22 would give us 95% power to detect 1.5-fold increases (Figure 18C) and >99% power to detect decreases of 1.5-fold or greater. In fact, with 22 embryos, we'd have a 90% chance of detecting a 1.33-fold (or 25%) decrease in expression (Figure 18D). This seems like a good deal to us and is experimentally feasible, so we decide ultimately to go with 22 embryos as our target sample size. In fact, this kind of back-and-forth negotiation with respect to sample size, sensitivity, and power is exactly what is supposed to take place. In any event, by carrying out the power analysis before we do our screen, we can be much more confident that our studies will be efficient and fruitful.
Although it may sound paradoxical, a larger-than-necessary sample size not only may be wasteful but also could lead to results that are grossly misleading. There are two reasons for this, one biological and one ethical. In the case of the former, large sample sizes can lead to statistically significant outcomes even when differences are so small in magnitude as to be biologically irrelevant. In this case, the detected difference is real, it's just not important. As previously stated, statistical significance should never be confused with biological significance. Unfortunately, some readers may be tempted to rely on the reported P-value as a kind of proxy for discerning the bottom line with respect to “significance” in the broader sense. Don't fall into this trap.
The ethical issue surrounding large sample sizes can be illustrated by a thought experiment. Imagine that you are testing for differences between two populations that are in fact identical for some trait of interest (admittedly, something you could never know beforehand). An initial sample size of 10 from each group shows a slight difference in means, as could be expected, but this difference isn't significant at the standard α level of 0.05. Not to be discouraged, you then increase each sample size by 10 and try the test again. If there is still no significant difference, you try adding another 10 and repeat the analysis. Will you eventually get a P-value ≤ 0.05? To answer this question, first recall the meaning of α = 0.05. Five percent of the time, the test will show a statistically significant difference even when the two populations are identical. Put another way, if you were to carry out 100 tests, each with a sample size of 10, 5 tests, on average, would give P ≤ 0.05 by random chance. Had you carried out 100 tests, would you only report the five that were significant? Hopefully not! Well, it turns out that that is effectively what you would be doing if you were to repeatedly increase your sample size with the intent of uncovering a positive finding. At some point, the two samples will show a statistically significant difference by chance—it's guaranteed! In fact, over the lifetime of such a “never-ending study”, chance differences will lead to P ≤ 0.05 5% of the time, P ≤ 0.01 1% of the time, and, if one were to be particularly persistent, a P-value of <0.001 could most certainly be achieved. Obviously the magnitude of the effects in this scenario would be very small (irrelevant in fact), but that won't matter to the statistical test. This kind of approach, sometimes referred to as an ad hoc, is clearly a major no-no, but it is a surprisingly easy trap to fall into. So remember that an experiment carried out ad infinitum will eventually give you a significant P-value even if none exists. Power analysis, as discussed above, can be a rational way to determine the necessary sample size in advance based on a specified α level and a pre-determined minimal difference of interest.
When it comes to outliers, there is no real consensus—not about how to formally define them, not about how best to detect them, and, most importantly, not about what to actually do with them. There is, of course, universal agreement that any data that are reported in the literature should be accurate and real. The slippery slope comes into play because discarding a data point that falls outside of the expected range of values also serves the purpose of yielding a cleaner, more appealing, and more statistically convincing result. In fact, getting rid of outliers, even ones that should likely be discarded, nearly always does just that. Note that we do not endorse the strategy of throwing out objectionable data points simply to make your results appear cleaner!
Outliers can arise in several ways. One is through incorrect data entry. Another is through experimental error, either on the part of the investigator or the apparatus being used. If there is good reason to believe that any data point, outlier or not, is likely to be flawed in either of these ways, getting rid of it is an easy call. Outliers, however, may also be legitimate, biologically correct data points that have occurred either through chance sampling or because the biology of the system is prone to producing such values. In fact, if it's the underlying biology that's driving things, this may turn out to be the most interesting outcome of the experiment.
Outliers principally affect statistics that are based on continuous variables, such as means and SDs, but do not generally have much of an impact on discrete or non-continuous variables, such as medians. For example, the median of the five values 4, 6, 7, 8, 10 is the same as the median of 4, 6, 7, 8, 235. In contrast, the means and SDs of these two data sets are very different. The resistance of median values to the effects of outliers provides a reasonable argument for using medians over means under certain circumstances. For example, in a subdivision with 100 houses, a mean value of $400,000 may be due to a handful of multi-million dollar properties. A median value of $250,000, however, might better reflect the cost of a typical home. Some problems with medians are that they are not as widely used in the scientific literature as means and also require a different set of statistical tools for their analysis. Specifically, the statistical analysis of medians is carried out using nonparametric approaches, such as a sign test, or through computational methods, such as bootstrapping (discussed below).
Concluding that an unexpected or anomalous value is an outlier deserving of banishment is not something that should ever be done informally. Some would argue that it's not something that should ever be done formally either. In any case, the danger of the informal or ad hoc approach is that our eyes, as well as our preconceptions, will identify many more outliers than really exist. In addition, our hopes and biases for certain experimental outcomes can cloud our judgment as to which values should be removed. Several formal tests can be used to identify “rejectable” outliers including the Grubb's outlier test and Dixon's Q test. These tests will answer the following question: Given a specified sample size, what is the probability that a value of this magnitude would occur assuming that the population from which the sample is derived is normally distributed? If this probability is ≤0.05, you then have legitimate grounds for tossing the data point. Alternatively, you can report your findings with and without the outlier present and let readers make up their own minds.
Outliers can also appear to be present in samples from populations that have lognormal distributions. In fact, without taking this into account, you could mistakenly reject a legitimate data point based on a statistical test that assumes normality. Lognormal distributions turn out to be quite common in biology. Whereas normal distributions result when many factors contribute additively to some measured outcome, lognormal distributions occur when factors act in a multiplicative fashion. Thus, sample data that appear to contain an outlier or otherwise look to be non-Gaussian, should be tested first by transforming the raw data into their corresponding log values and plotting them on a histogram. If the distribution of the transformed values looks normal, then the original distribution was probably lognormal. To handle things statistically, you can use the log-transformed data to carry out tests that assume normality. Back-transformations to the linear scale can also be carried out if necessary to report certain values. In the case of means, this will produce a parameter referred to as the geometric mean, which (like the median) will tend to give values that are more typical of the data set. For example, we can transform the numbers 6, 12, 19, 42, and 951 to their log10 values (0.78, 1.1, 1.3, 1.6, 3.0), calculate their mean (1.55), and then back-transform (10x) to get a geometric mean of 35.3, which differs substantially from the standard or arithmetic mean of 206.
Another approach, which may be particularly well suited to handling situations where inconsistent or spurious data tend to arise at either end of the spectrum, is to use trimmed or truncated data. For example, a 10% trimmed mean would remove 10% of the highest values AND 10% of the lowest values. Thus, for the series 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, both 1 and 10 would be removed before calculating the mean. This method can provide more information than the median61 but is conveniently resistant to the effects of outliers. An example of an appropriate use for a trimmed mean might involve quantifying protein expression in C. elegans embryos using immunostaining. Even if done carefully, this method can result in a small fraction of embryos that have no staining as well as some that appear to have high levels of non-specific staining. Thus, the trimmed mean would provide a reasonable measure of the central tendency of the dataset.
Most of the tests described in the above sections rely on the assumption that the data are sampled from populations with relatively normal distributions62. Such tests, which include the t-test, are referred to as parametric tests. Nonparametric tests should be used if the population distributions are known to deviate or are suspected to deviate far from normality. In addition, nonparametric tests may be appropriate if a population deviates only moderately from a normal distribution but the sample size is insufficient to compensate for this at the level of the distribution of the statistic. Although it would be nice to be able to provide some cut-and-dry criteria for making a call regarding when to use parametric versus nonparametric tests, the minimum sample size required for conducting a parametric test will depend on the degree to which the underlying population deviates from normality. The larger the deviation, the larger the sample size must be for parametric tests to be valid. Although some texts recommend a sample size of 30 as being safe, this may be insufficient if the population distribution is very far from normal. Nonparametric tests are also required when statistics are to be carried out on discontinuous parameters such as medians.
The basis for many nonparametric tests involves discarding the actual numbers in the dataset and replacing them with numerical rankings from lowest to highest. Thus, the dataset 7, 12, 54, 103 would be replaced with 1, 2, 3, and 4, respectively. This may sound odd, but the general method, referred to as a sign test, is well grounded. In the case of the Mann-Whitney test, which is used to compare two unpaired groups, data from both groups are combined and ranked numerically (1, 2, 3, … n). Then the rank numbers are sorted back into their respective starting groups, and a mean rank is tallied for each group63. If both groups were sampled from populations with identical means (the null hypothesis), then there should be relatively little difference in their mean ranks, although chance sampling will lead to some differences. Put another way, high- and low-ranking values should be more or less evenly distributed between the two groups. Thus for the Mann-Whitney test, the P-value will answer the following question: Based on the mean ranks of the two groups, what is the probability that they are derived from populations with identical means? As for parametric tests, a P-value ≤ 0.05 is traditionally accepted as statistically significant.
The obvious strength of nonparametric tests is that they allow an investigator to conduct a statistical analysis that would otherwise not be possible (or at least valid) using traditional parametric tests. A downside is that nonparametric tests are somewhat less powerful than parametric tests and so should be applied only when necessary64. The reduced power is due to the fact that quantitative information is discarded when ranks are assigned. In addition, nonparametric tests will often lack the ability to provide CIs, which can be quite useful. Finally, nonparametric tests can underestimate the effects of outliers, which may be valid data points and biologically significant. Below is a brief list of some common nonparametric tests and their applications. Note that although these are so-called nonparametric tests, most do require certain assumptions about the data and collection methods for their results to be valid. Be sure to read up on these methods or consult a statistician before you apply them.
The Mann-Whitney test (a.k.a. Wilcoxon rank-sum test, Mann-Whitney U-test, and sign test) is used in the place of a two-sample t-test to compare two groups. Variations on this theme are also used to test for differences in medians.
The Wilcoxon matched pairs signed-rank test (a.k.a. Wilcoxon's test and Wilcoxon signed-rank test) is used in place of the paired t-test for matched data.
The one-sample sign tool, which is similar to a one-sample t-test, is used for medians and can also provide CIs. No major assumptions are required.
The one-sample Wilcoxon signed-rank test has the same applications as the one-sample sign tool but is more powerful. It does, however, assume that the distribution of values is symmetric around the median.
The Kruskal-Wallis test is used in place of a one-way ANOVA.
The rank correlation test (a.k.a. Spearman's rank correlation coefficient and Spearman's rho) is used in place of linear correlation.
The logrank test (a.k.a. Mantel Cox method) is used to compare survival curves.
In the fields of aging and stress, it is common to compare two or more strains for differences in innate laboratory lifespan or in survival following an experimental insult. Relative to studies on human subjects, survival analysis in C. elegans and other simple laboratory organisms is greatly simplified by the nature of the system. The experiments generally begin on the same day for all the subjects within a given sample and the study is typically concluded after all subjects have completed their lifespans. In addition, individual C. elegans rarely need to be censored. That is they don't routinely move way without leaving a forwarding address (although they have been known to crawl off plates) or stop taking their prescribed medicine.
One relatively intuitive approach in these situations would be to calculate the mean duration of survival for each sample along with the individual SDs and SEs. These averages could then be compared using a t-test or related method. Though seemingly straightforward, this approach has several caveats and is not recommended (Suciu et al., 2004). One issue is that survival data are often quite skewed, and therefore tests that rely on assumptions of normality (e.g., the t-test) may not be valid. A second is that the t-test will have less power than some well-accepted alternative tests to detect small, but biologically meaningful, differences between populations. Another possible approach would be to focus on differences in survival at just one or perhaps several selective time points. However, this approach has the disadvantage of superficially appearing to be arbitrary, and it also fails to make use of all the available data.
The preferred alternative to the approaches discussed above is to make use of statistical tests that compare viability over the duration of the entire experiment, wherein each time point represents a cumulative opportunity to detect differences. For the C. elegans field, this can be accomplished using a standard version of the logrank test. The null hypothesis of the logrank test is that there is no difference in survival (or some other trait of interest) between the two populations under study. Thus, a trend of consistent differences over time would lead to rejection of the null hypothesis and a statistically significant finding. The logrank test is mathematically accomplished in part by combining the survival data from both populations and using this value to calculate the expected number of events (such as deaths) that would be predicted to occur in each population at each time point.
For example, from starting samples of 20 worms each, if five deaths occurred in strain A and one death occurred in strain B on day 1, then the total number of deaths on day 1 would be six. In this case, the predicted number of deaths for each strain on day 1 is simply the average of the two strains, namely three deaths. Thus, the difference between the observed and expected (Eobs – Eexp) deaths for strain A is 2 (5 − 3 = 2) and is −2 for strain B (1 − 3 = −2). These calculations get slightly more cumbersome at subsequent time points because adjustments must be made to compensate for differences in sample sizes at the start of each day (only the viable animals remain to be sampled), but the principle remains the same65. In this example, if the frequency of death in strain A was authentically higher, then summing the differences from each day (until the strain A sample had perished entirely) should give a positive number. If this number were sufficiently large66 then a low P-value would be detected. If daily differences were due only to chance, however, it would be expected that a roughly equal number of positive and negative differences would be obtained over the course of the experiment, and thus the summed values would be close to zero, leading to a high P-value (e.g., >0.05). It is important to note that this test as described above is always between two populations, and thus the two populations tested should be explicitly stated for each P-value. Furthermore, issues of multiple comparisons should be taken into account when multiple samples are being compared.
I (DF) have it on good word (from KG) that if statistics were being invented today, bootstrapping, as well as related re-sampling methods, would be the standard go-to approach. The reason that the statistics field took so long to come up with bootstrapping is forgivable. Until very recently, the computing power required to run resampling methods was unfathomable. Had statistics been invented in the last 10 years, however, the central statistical principles that underlie most of our favorite tests would probably be relegated to the side stream of mathematical curiosities as interesting but obscure numerical properties of interest only to theoreticians. Because the genesis and much of the development of statistics took place in the absence of powerful computers we are still, however, entrenched in what could be viewed as an outdated way of doing things. This is not to suggest that the old ways don't work quite well. In fact, they usually give answers that are nearly identical to those provided by the newer computationally intensive methods. The newer methods, however, require fewer assumptions and are therefore more broadly applicable and have fewer associated caveats. In particular, re-sampling methods do not require that the data be sufficiently normal. As such, bootstrapping and related approaches are in fact nonparametric methods67. Re-sampling methods can also be applied to statistical parameters that are not handled well by traditional methods, such as the median. Differences between the re-sampling methods and the nonparametric approaches outlined above are that re-sampling methods are not limited to the use of ranked-sign data and can therefore be applied to a wider range of statistical parameters, such as CIs. These properties mean that re-sampling methods have greater statistical power and flexibility than traditional nonparametric approaches. All this points to a future where re-sampling methods will largely rule the day. Get ready.
The basic idea of bootstrapping is to use a sample dataset of modest size to simulate an entire population. An example is provided by carrying out calculations to derive a 95% CI of the mean using the data that were analyzed in Figure 5A (Section 2.2; Figure 19). Here, 55 data points comprise the original sample of measured GFP intensities. In the first round of bootstrapping, the 55 data points are randomly re-sampled with replacement to obtain a new data set of 55 values (Figure 19). Notice that, by sampling randomly with replacement, some of the data points from the original dataset are missing, whereas others are repeated two or more times. A mean is then calculated for the re-sampled set, along with other statistical parameters that may be of interest. Round one is done. The results of rounds two and three are also shown for clarity (Figure 19). Now repeat 3,997 more times. At this point, there should be 4,000 means obtained entirely through re-sampling. Next, imagine lining up the 4,000 means from lowest to highest, top to bottom (Figure 19). We can partition off the lowest (top of list) 2.5% of values by drawing a line between the mean values at positions 100 and 101. We can also do this for the highest (bottom of list) 2.5% of values by drawing a line between the means at positions 3,900 and 3,901. To get a 95% CI, we simply report the mean values at positions 101 (14.86890) and 3900 (19.96438). Put another way, had we carried out just 40 iterations68 instead of 4,000, the 95% CI would range from the second highest to the second lowest number. Thus, at its core, bootstrapping is conceptually very simple69. The fact that it's a bear computationally matters only to your computer.
Figure 19. Illustration of the bootstrap process. The original dataset is the one used for Section 2.2, Figure 5A.
The 4,000 individual means obtained through re-sampling can also be used to construct a histogram, which you may notice looks strikingly similar to a normal curve (Figure 20). Not surprisingly, the apex of the curve corresponds very closely to the mean value of the original 55 data points (17.32; Figures 5A and 19). Furthermore, if we examine the values at approximately two SDs (1.96 to be exact) to either side of the red vertical lines in Figure 20, we obtain 14.7 and 19.9, which again correspond closely to the 95% CI obtained by bootstrapping (14.9, 20.0) as well as the 95% CI obtained through traditional approaches (14.6 and 20.0; Figure 5A). Thus, at some level, bootstrapping dovetails with some of the concepts covered in earlier sections, such as the idea of obtaining normal distributions through theoretical repeated sampling (Section 2.6). In fact, one of the methods to check the validity of data obtained from bootstrap methods is to generate histograms such as the one in Figure 20.
Figure 20. Bootstrapped sampling distribution of the mean. A normal curve (blue line) has been inserted for reference. Red vertical lines indicate 95% CI boundaries (∼2 SDs to either side of the mean)
Re-sampling methods can also be applied to test for differences in means between two independent samples, a process generically referred to as permutation tests. In this case, data from the two samples are first combined into one set. For example, samples with 22 and 58 data points would be combined to give a single sample of 80. Next, re-sampling without replacement is carried out to generate two new samples of size 22 and 58. Because the re-sampling is done without regard to which group the original data points came from, this will result in a random re-shuffling of the data points into the two groups. Next, means are obtained for each of the new sample sets and the difference between these means is calculated. Round one is now done. The original set of 80 is then resampled thousands more times. A P-value for the difference between means is then derived by noting the proportion of times that the two resampled sets gave mean differences that were as large or larger than the difference between the original datasets. If a P-value that was ≤ 0.05 resulted, the difference would typically be deemed statistically significant. Thus, much like the bootstrap calculation of the 95% CI, the re-sampling method is actually more simple and intuitive to grasp then the classical statistical methods, which rely heavily on theory70.
Because bootstrapping takes a single experiment with a limited sample size and effectively turns it into many thousands of experiments, some skeptical scientists may suspect bootstrapping to constitute a form of cheating. Of course this isn't true. That said, whenever you make any inference regarding the population as a whole from a single sample of that population, some assumptions are required. In the case of using classical statistical methods, such as those that rely on the t, z, and other distributions, we are assuming that the sample statistic that we are estimating has a roughly normal distribution. Moreover, the conclusions we derive using these methods are based on the impossible scenario that we carry out the experiment an infinite number of times. Thus, although we tend to accept these standard methods, assumptions are certainly inherent. Bootstrapping is no different. Like the classical methods, it uses the sample data to estimate population parameters. However, instead of using theoretical distributions, such as z and t, we use re-sampling of the data to predict the behavior of the sample statistic. Moreover, in the case of bootstrapping, we don't have to assume that the distribution of our statistic is normal. Therefore, bootstrapping actually requires fewer assumptions than classical methods and is consequently more reliable. Of course, if the experiment wasn't conducted well (non-random or inaccurate sampling methods) or if the numbers are very low, then neither classical nor bootstrapping methods will give reliable results. Statistics cannot validate or otherwise rescue a scientifically flawed experiment.
60An online document describing this issue is available at: firstclinical.com/journal/2007/0703_Power.pdf. In addition, a recent critical analysis of this issue is provided by Bacchetti (2010).
61The median is essentially a trimmed mean where the trimming approaches 100%!
62More accurately, the tests assume that the populations are normal enough and that the sample size is large enough such that the distribution of the calculated statistic itself will be normal. This was discussed in Section 1.
63Note that there are subtle variations on this theme, which (depending on the text or source) may go by the same name. These can be used to test for differences in additional statistical parameters such the median.
64More accurately, nonparametric tests will be less powerful than parametric tests if both tests were to be simultaneously carried out on a dataset that was normal. The diminished power of nonparametric tests in these situations is particularly exacerbated if sample sizes are small. Obviously, if the data were indeed normal, one would hopefully be aware of this and would apply a parametric test. Conversely, nonparametric tests can actually be more powerful than parametric tests when applied to data that are truly non-Gaussian. Of course, if the data are far from Guassian, then the parametric tests likely wouldn't even be valid. Thus, each type of test is actually “better” or “best” when it is used for its intended purpose.
65For example, strains A and B might have six and twelve animals remaining on day 5, respectively. If a total of three animals died by the next day (two from strain A and one from strain B) the expected number of deaths for strain B would be twice that of A, since the population on day 5 was twice that of strain A. Namely, two deaths would be expected for strain B and one for strain A. Thus, the difference between expected and observed deaths for strains A and B would be 1 (2−1=1) and −1 (1−2=−1), respectively.
66The final calculation also takes into account sample size and the variance for each sample.
67Note that, although not as often used, there are also parametric bootstrapping methods.
68This is a bad idea in practice. For some statistical parameters, such as SE, several hundred repetitions may be sufficient to give reliable results. For others, such as CIs, several thousand or more repetitions may be necessary. Moreover, because it takes a computer only two more seconds to carry out 4,000 repetitions than it takes for 300, there is no particular reason to scrimp.
69Note that this version of the procedure, the percentile bootstrap, differs slightly from the standard bootstrapping method, the bias corrected and accelerated bootstrap (BCa). Differences are due to a potential for slight bias in the percentile bootstrapping procedure that are not worth discussing in this context. Also, don't be unduly put off by the term “bias”. SD is also a “biased” statistical parameter, as are many others. The BCa method compensates for this bias and also adjusts for skewness when necessary.
70A brief disclaimer. Like everything else in statistics, there are some caveats to bootstrapping along with limitations and guidelines that one should become familiar with before diving into the deep end.
We greatly appreciate input from Naomi Ward on the contents of this review. We are particularly indebted to Amy Fluet for editing this ungainly monolith and providing much useful critique. We also thank Oliver Walter for encouraging this project and both anonymous reviewers for taking on this task and providing constructive comments. This work was supported by NIH grant GM066868.
Agarwal, P., and States, D.J. (1996). A Bayesian evolutionary distance for parametrically aligned sequences. J. Comput. Biol. 3, 1–17. Abstract Article
Agresti, A., and Coull, B.A. (1998). Approximate is better than Exact for Interval Estimation of Binomial Proportions. The American Statistician 52, 119–126. Article
Agresti, A., and Caffo, B. (2000). Simple and effective confidence intervals for proportions and differences of proportions result from adding two successes and two failures. The American Statistician 54, 280–288. Article
Bacchetti P. (2010). Current sample size conventions: flaws, harms, and alternatives. BMC Med. 8, 17. Abstract Article
Benjamini, Y., and Hochberg. Y. (1995). Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. Roy. Statist. Soc. Ser. B Stat. Methodol. 57, pp. 289–300. Article
Brown, L.D., Cai, T., and DasGupta, A. (2001). Interval estimation for a binomial proportion. Statist. Sci. 16, 101–133. Article
Burge, C., Campbell, A.M., and Karlin, S. (1992). Over- and under-representation of short oligonucleotides in DNA sequences. Proc. Natl. Acad. Sci. U. S. A. 89, 1358-1362. Abstract
Carroll, P.M., Dougherty, B., Ross-Macdonald, P., Browman, K., and FitzGerald, K. (2003) Model systems in drug discovery: chemical genetics meets genomics. Pharmacol. Ther. 99, 183-220. Abstract Article
Doitsidou, M., Flames, N., Lee, A.C., Boyanov, A., and Hobert, O. (2008). Automated screening for mutants affecting dopaminergic-neuron specification in C. elegans. Nat. Methods 10, 869–72. Article
Gassmann, M., Grenacher, B., Rohde, B., and Vogel, J. (2009). Quantifying Western blots: pitfalls of densitometry. Electrophoresis 11, 1845–1855. Article
Houser, J. (2007). How many are enough? Statistical power analysis and sample size estimation in clinical research. J. Clin. Res. Best Pract. 3, 1-5. Article
Hoogewijs, D., De Henau, S., Dewilde, S., Moens, L., Couvreur, M., Borgonie, G., Vinogradov, S.N., Roy, S.W., and Vanfleteren, J.R. (2008). The Caenorhabditis globin gene family reveals extensive nematode-specific radiation and diversification. BMC Evol. Biol. 8, 279. Abstract Article
Jones, L.V., and Tukey, J. (2000). A sensible formulation of the significance test. Psychol. Methods 5, 411–414. Abstract Article
Kamath, R.S., Fraser, A.G., Dong, Y., Poulin, G., Durbin, R., Gotta, M., Kanapin, A., Le Bot, N., Moreno, S., Sohrmann, M., Welchman, D.P., Zipperlen, P., and Ahringer, J. (2003). Systematic functional analysis of the Caenorhabditis elegans genome using RNAi. Nature 16, 231–237. Abstract Article
Knill, D.C, and Pouget, A. (2004). The Bayesian brain: the role of uncertainty in neural coding and computation. Trends Neurosci. 12, 712-719. Abstract Article
Nagele, P. (2003). Misuse of standard error of the mean (SEM) when reporting variability of a sample. A critical evaluation of four anaesthesia journals. Br. J. Anaesth. 4, 514-516. Abstract Article
Ramsey, F.L. and Schafer, D.W. (2013). The Statistical Sleuth: a Course in Methods of Data Analysis, Third Edition. (Boston: Brooks/Cole Cengage Learning).
Shaham, S. 2007. Counting mutagenized genomes and optimizing genetic screens in Caenorhabditis elegans. PLoS One 2, e1117. Abstract
Suciu, G.P., Lemeshow, S., and Moeschberger, M. (2004). Hand Book of Statistics, Volume 23: Advances in Survival Analysis, N. Balakrishnan and C.R. Rao, eds. (Amsterdam: Elsevier B. V.), pp. 251-261.
Sulston, J.E., and Horvitz, H.R. (1977). Post-embryonic cell lineages of the nematode, Caenorhabditis elegans. Dev. Biol. 56, 110–156. Abstract Article
Sun, X., and Hong, P. (2007). Computational modeling of Caenorhabditis elegans vulval induction. Bioinformatics 23, i499-507. Abstract Article
Note: these tools require the Microsoft Windows operating system. Information about running Windows on a Mac (Apple Inc.) can be found at http://store.apple.com/us/browse/guide/windows.
Motulsky, H. (2010). Intuitive Biostatistics: A Nonmathematical Guide to Statistical Thinking, Second Edition (New York: Oxford University Press).
This is easily my favorite biostatistics book. It covers a lot of ground, explains the issues and concepts clearly, and provides lots of good practical advice. It's also very readable. Some may want more equations or theory, but for what it is, it's excellent. (DF)
Triola M. F., and Triola M.M. (2006). Biostatistics for the Biological and Health Sciences (Boston: Pearson Addison-Wesley).
This is a comprehensive and admirably readable conventional statistical text book aimed primarily at advanced undergraduates and beginning graduate students. It provides many great illustrations of the concepts as well as tons of worked examples. The main author (M. F. Triola) has been writing statistical texts for many years and has honed his craft well. This particular version is very similar to Elementary Statistics (10th edition) by the same author. (DF)
Gonick, L. and Smith, W. (1993). The Cartoon Guide to Statistics (New York: HarperPerennial).
Don't let the name fool you. This book is quite dense and contains the occasional calculus equation. It's an enjoyable read and explains some concepts very well. The humor is corny, but provides some needed levity. (DF)
van Emden, H. (2008). Statistics for Terrified Biologists (Malden, MA: Blackwell Publishing).
This paperback explains certain concepts in statistics very well. In particular, its treatment of the theory behind the T test, statistical correlation, and ANOVA is excellent. The downside is that the author operates under the premise that calculations are still done by hand and so uses many shortcut formulas (algebraic variations) that tend to obscure what's really going on. In addition, almost half of the text is dedicated to ANOVA, which may not be hugely relevant for the worm field. (DF)
Sokal R. R., and Rohlf, F. J. (2012). Biometry: The Principles and Practice of Statisticsin Biological Research, Fourth Edition (New York: W. H. Freeman and Co.).
One of the “bibles” in the field of biostatistics. Weighing in at 937 pages, this book is chock full of information. Unfortunately, like many holy texts, this book will not be that easy for most of us to read and digest. (DF)
Ramsey, F.L. and Schafer, D.W. (2013). The Statistical Sleuth: a Course in Methods of Data Analysis, Third Edition. (Boston: Brooks/Cole Cengage Learning).
Contemporary statistics for a mature audience (meaning those who do real research), done with lots of examples and explanation, and minimal math. (KG)
Fay, D.S., and Gerow, K. (2013). A biologist's guide to statistical thinking and analysis. WormBook, ed. The C. elegans Research Community, WormBook,
Quite simply a tour de farce, written by two authors with impeachable credentials and a keen eye for misguiding naïve biologists.
Minitab
A comprehensive and reasonably intuitive program. This program has many useful features and is frequently updated. The downside for Mac users is that you will have to either use a PC (unthinkable) or run it on parallels (or some similar program) that lets you employ a PC interface on your Mac (shudder). (DF)
Microsoft Excel
Excel excels at doing arithmetic, but is not meant to be a statistics package. It does most simple things (t-tests) sort of reasonably well, but the interface is clunky. Minitab (or any other stats package) would be preferred. (KG)
There are many such sites, which have the advantage of being free and generally easy to use. Of course, what is available at the time of this writing could change rapidly and without notice. As with anything else that's free on the web, rely on at your own risk!
*Edited by Oliver Hobert. Last revised January 14, 2013, Published July 9, 2013. This chapter should be cited as: Fay D.S. and Gerow K. A biologist's guide to statistical thinking and analysis (July 9, 2013), WormBook, ed. The C. elegans Research Community, WormBook, doi/10.1895/wormbook.1.159.1, http://www.wormbook.org.
Copyright: © 2013 David S. Fay and Ken Gerow. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
§To whom correspondence should be addressed. Email: davidfay@uwyo.edu
 All WormBook content, except where otherwise noted, is licensed under a Creative Commons Attribution License.
All WormBook content, except where otherwise noted, is licensed under a Creative Commons Attribution License.